·快速排序（O(nlogn)）

快排的思路是选一个基准元素A，比A大的放A右边，比A小的放A左边。然后再按这个方式对A左右两边的子序列操作。该排序法使用了分治法。该算法的时间复杂度为O(logn)。

 

基准元素一般选取第一个元素。但如果序列是倒序的，那么基准元素选第一个元素会发现每一轮排完之后，基准元素的一边是全部元素，另一边没有元素。此时算法复杂度会退化为O(n^2)。为了避免这种情况我们可以每次递归的时候随机取序列的一个元素为基准元素而不是取第一个元素。

 

下面我们看看快排的具体过程和思路，主要还是运用了滑动窗口的思想技巧。我们定义两个指针p1,p2，区间范围[p1, p2]表示滑动窗口，滑动窗口被明确定义为只能放大于等于基准元素midEle。随后p2不断向后移动，扩大窗口，并探测新进入窗口的元素arr[p2]是否大于等于基准元素，arr[p2] >= midEle则不作任何动作，arr[p2] < midEle则需要把arr[p2]移出窗口，移到窗口左侧的区域，具体做法是将arr[p1]和arr[p2]互换并将p1向后移动一格，缩小窗口。

 

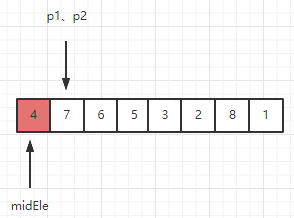
1、一开始基准元素为midEle, p1,p2重合，滑动窗口内初始序列为[7]。检测新元素7 > midEle，因此 7 满足能呆在滑动窗口的条件。

 

 

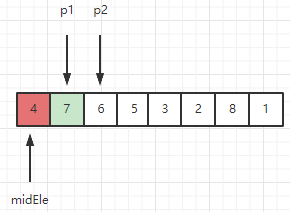
2、此时窗口内序列为 [7, 6]， 检测新元素6 > midEle，因此 6 满足能呆在滑动窗口的条件。继续如上操作，将5也纳入窗口内，当p2指到元素3的时候，往下看步骤3。

 

 

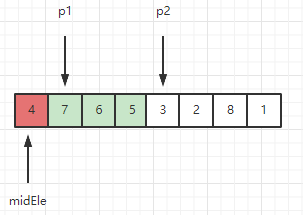
2、此时窗口内序列为 [7, 6, 5, 3]， 检测新元素3 < midEle，因此 3 不满足呆在滑动窗口的条件，需要把3挪出窗口。挪动操作如下所示：

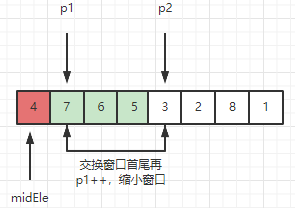
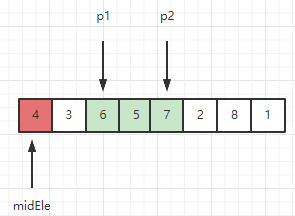
更新后，窗口为 [6, 5, 7]。

 

接下来重复上述过程，直到p2溢出数组。

 

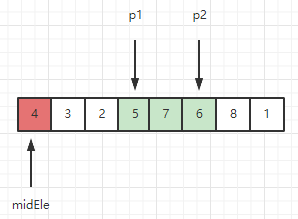
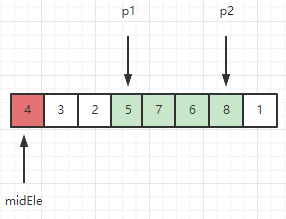
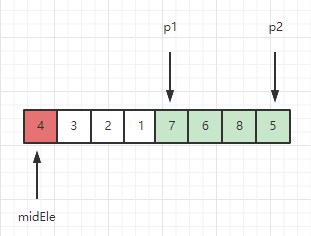
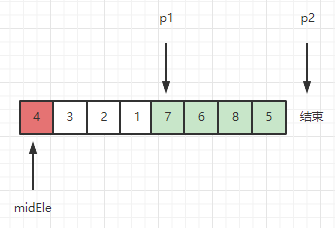
此时 [1, p1) 和 [7, len(arr)-1] 分别是小于midEle的部分 和 大于等于midEle的部分，需要将4放到这两个区域之间：

 

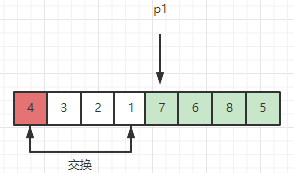
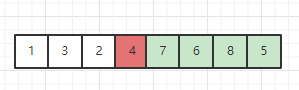
之后再对中间元素 4 以左和以右的子序列递归操作即可。

 

代码实现如下：

func quickSortWin(arr []int){
	if len(arr) <= 1{
		return
	}

	midEleIdx := rand.Intn(len(arr))
	midEle := arr[midEleIdx]
	arr[0], arr[midEleIdx] = arr[midEleIdx], arr[0]
	var p1, p2 int    // 滑动窗口，里面是大于等于midEle的元素

	for p1, p2 = 1, 1; p2 < len(arr); p2++{
		if midEle > arr[p2]{
			arr[p2], arr[p1] = arr[p1], arr[p2]
			p1++	// 缩小窗口
		}
	}

	arr[0], arr[p1-1] = arr[p1-1], arr[0]
	quickSortWin(arr[:(p1-1)])
	quickSortWin(arr[p1:])
}

 

使用滑动窗口技巧是我能想到的最容易理解快排的方法。实际上双指针技巧和滑动窗口还可以用来解决很多其他的数组问题。

 

最后附上非递归版本的快排，使用栈实现

type QuickSortNode map[string]int
func quickSortWinWithStack(arr []int){
	stack := list.InitLinkedList()
	stackVal := QuickSortNode{"startIdx":0, "endIdx":len(arr) - 1}
	stack.UnShift(stackVal)
	var p1, p2 int    // 滑动窗口

	for stack.Length > 0{
		curStackVal := stack.Shift().(QuickSortNode)
		startIdx := curStackVal["startIdx"]
		endIdx := curStackVal["endIdx"]

		midEleIdx := startIdx + rand.Intn(endIdx-startIdx+1)
		midEle := arr[midEleIdx]
		arr[startIdx], arr[midEleIdx] = arr[midEleIdx], arr[startIdx]


		for p1, p2 = startIdx + 1, startIdx + 1; p2 <= endIdx; p2++{
			if midEle > arr[p2]{
				arr[p2], arr[p1] = arr[p1], arr[p2]
				p1++	// 缩小窗口
			}
		}

		arr[startIdx], arr[p1-1] = arr[p1-1], arr[startIdx]
		if p1 - 1 > startIdx{
			stackVal = QuickSortNode{"startIdx":startIdx, "endIdx":p2-2}
			stack.UnShift(stackVal)
		}

		if p1 < endIdx{
			stackVal := QuickSortNode{"startIdx":p1, "endIdx":endIdx}
			stack.UnShift(stackVal)
		}
	}
}