· KMP算法思路

KMP算法也是通过减少字符串匹配的轮数进行优化的，BM算法关注“坏字符”和“好后缀”，KMP算法关注“已匹配的前缀”。

KMP算法的思路是：将主串A的子串与模式串B进行多轮匹配，每轮匹配中从前往后比对字符，需要将AB的已匹配串中的相同B前缀串和A后缀串对齐，从而跳过若干轮匹配。

具体步骤：

1、把主串和模式串的首位对齐，从前到后对逐个字符进行比较，得到第一个坏字符，坏字符之前的内容就是已匹配前缀，已匹配前缀是 “GTGTG”。

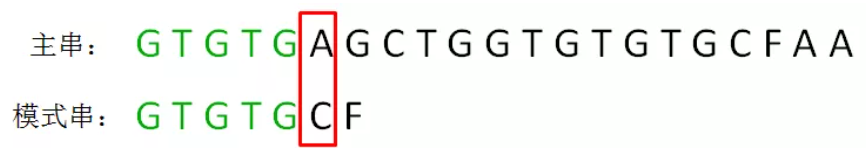
2、需要从已匹配前缀中找到A的最长可匹配后缀子串和B的最长可匹配前缀子串（下面简称为 匹配前缀 和 匹配后缀），即GTG，将他们对齐。

3、重复上述过程，确定新的已匹配前缀GTG，和它的匹配后缀与匹配前缀，即G，并对齐：

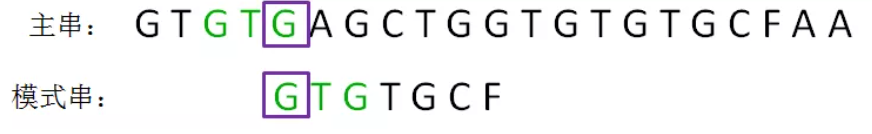
然后继续从对齐的位置往后进行字符比较。由于 "T" != “A”，因此 “A”是个坏字符，已匹配前缀串G是个单字符的字符串，没有匹配前缀和后缀。

4、如果没有已匹配前缀（即第一个字符就不匹配）则模式串B只往后移动一位；如果已匹配前缀串中没有相同的匹配前缀和匹配后缀，则模式串B往后移动已匹配前缀串的位数。

重复上述过程。

什么是最长可匹配后缀（子串）和最长可匹配前缀（子串）？如果一个字符串x，x的后缀子串y也是它的前缀子串z，而且x和z本身≠y，那么这个子串x就是最长可匹配前缀子串同时也是最长可匹配后缀子串。

例如 ABCA 的最长可匹配前缀为"A"，ABCAB 的最长可匹配前缀为"AB"。GTGTG的最长可匹配前缀是“GTG”。

· KMP预处理

KMP算法的关键是预处理得到模式串B所有 前缀子串 的匹配前缀和匹配后缀。

本例中的模式串B是 “GTGTGCF”，它所有的前缀子串 B[:i] 包括

“”，“G”，“GT”，“GTG”，“GTGT”，“GTGTG”，“GTGTGC”，“GTGTGCF”。因此一个长度是 n 的字符串，它的已匹配子串的个数为n+1。

举个例子：模式串B（“GTGTGCF”）的一个前缀子串 “GTGT”，它的匹配前缀是 “GT”。

匹配前缀和后缀只和模式串B自己有关，和主串无关。

预处理过程如下：

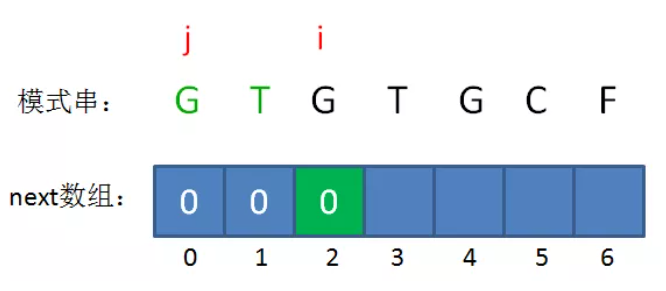
构建一个next数组，next[i]表示B中长度为 i 的前缀子串的可匹配前缀串的后一个字符的下标（i∈[1, len(B)]），B[:i]表示长度为 i 的前缀子串。

B[:next[i]]就是B[:i]的最长可匹配前缀串。

例如：GTGTGCF的一个已匹配子串GTGTG，i=5，它的最长可匹配前缀"GTG"的下一个字符是"T"，所以 next[5] = 3。

next数组的构建是一个动态规划的过程，next[i]依赖于next[j]（k<i)。

假设有一个字符串 M，有两种情况：

如果 M 的最后一个字符b1 等于 M[:len(M)-1]这个字符串的匹配前缀的下一个字符b2。则M的匹配前缀就是M[:len(M)-1]的匹配前缀串+b2。否则 M[:len(M)-1]的匹配前缀的下一个字符b2 要回溯到M[:len(M)-2]的匹配前缀的下一个字符b3，判断b1和b3是否相同。

举个例子，已知 M = "GTGG"，求next[4] = ?

M = "GTGG"，M[:len(M)-1] = "GTG"，M的最后一个字符是"G"，M[:len(M)-1]的匹配前缀是M[0]这个"G"，它的下一个字符是M[1] = "T"；

"G" != "T" => 回溯 => M[:len(M)-2] = "GT", M[:len(M)-2]的匹配前缀是空字符串，它的下一个字符是M[0] = "G"；

"G" == "G"，所以 M的匹配前缀是“G”，它的下一个字符"T"。因此next[4] =1

写为公式就是：

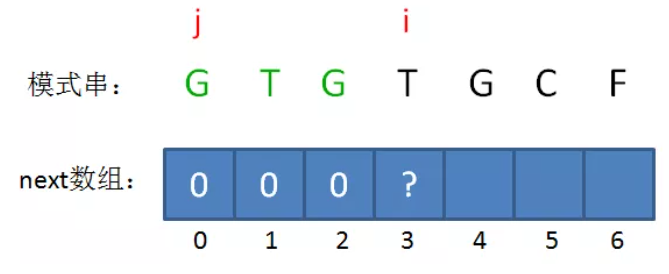
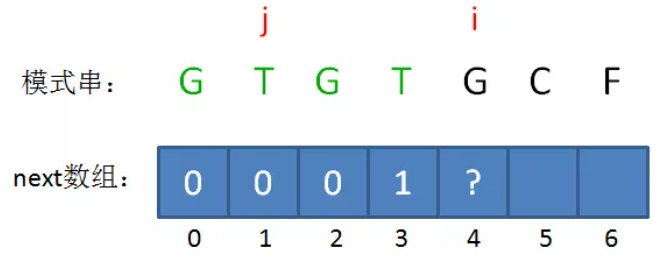
欲求next[i]，先得到 j = next[i-1]

1、如果 B[i-1] == B[j]，则next[i] = j+1；

2、如果B[i-1] != B[j]，则 j = next[i-2]（回溯）并循环判断B[i-1] != B[j]，如果判断成功则 。

​​​​​​​

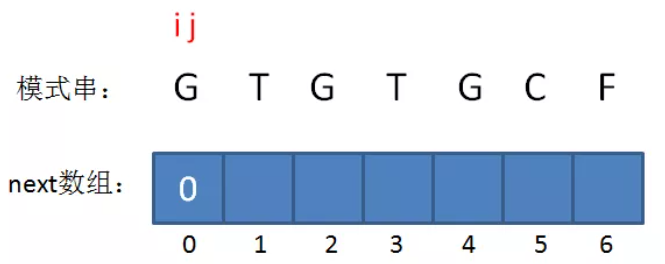
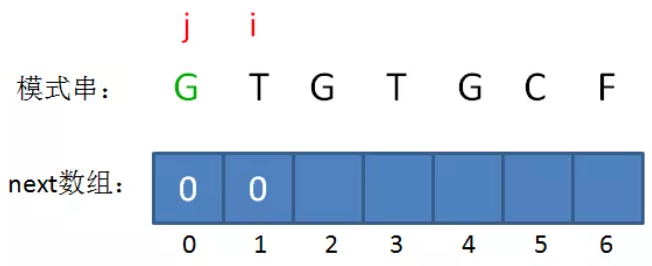
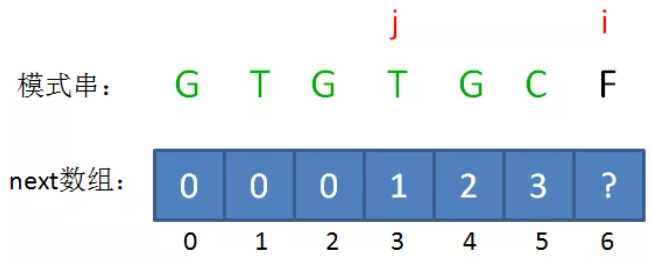
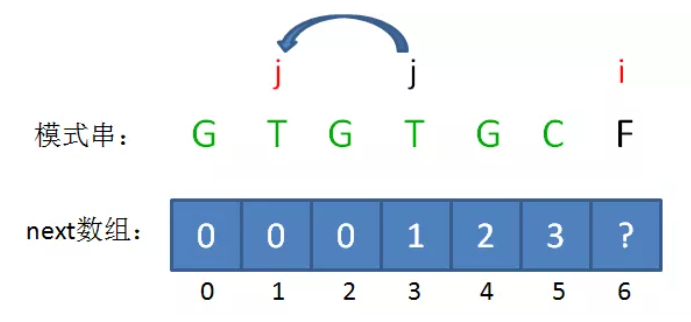
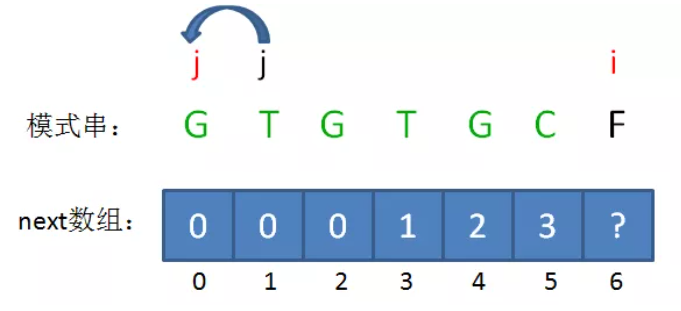
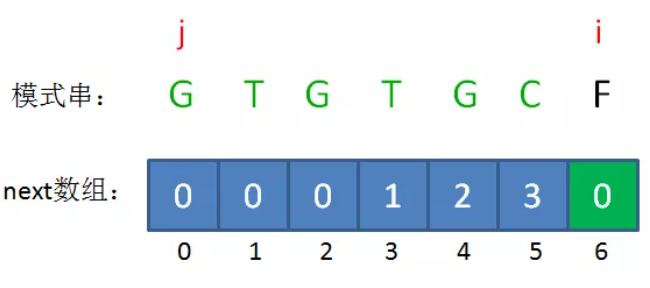
如果B的长度为n，则next的大小也为n，即next只记录B的前n-1个长度的解，不记录B本身的解，因为如果前缀子串就是B本身，那么本轮匹配已经成功，无需再找其匹配前缀。

下面是KMP算法：

func KMP(a, b string) int{
	if len(b) > len(a){
		return -1
	}

	next := _getNexts(b)	// 生成next数组
	start := 0 				// start是主串中要和模式串匹配的子串的首字符位置
	des := len(a) - len(b)
	j := 0		// j是本轮匹配中已匹配字符的下一个字符下标

	for start <= des{ 
		for i:=j; i<len(b); i++{
			if b[i] != a[start + i]{	// 如果匹配到坏字符时，已匹配字符个数大于0，则将b后移若干位使得a中的坏字符位置和b的最长匹配前缀的下一个字符位置对齐
				if j != 0{
					start = start + (i - next[i])		// 代码的直接意思是将a中的坏字符位置和b的最长匹配前缀的下一个字符位置对其（等价于将 b中的最长匹配前缀和a中的最长匹配后缀对其）
				}else{	// 如果匹配到坏字符时，已匹配字符个数为0，则b往后移一位
					start++
				}
				j = next[i]
				break
			}else{
				j++
			}
		}
		if j == len(b){		// 说明整个模式串b所有字符都比对成功
			return start
		}
	}
	return -1
}

func _getNexts(b string) []int{
	next := make([]int, len(b))
	next[0], next[1] = 0, 0
	j := 0

	for i:=2; i<len(b);i++{
		for j > 0 && b[i-1] != b[j]{
			j = next[j]		// j回溯到上一个匹配前缀（的下一个字符位置）
		}

		// 走到这里有两种情况，一是 b[i-1] == b[j]， 一是j == 0 但还不知道是否 b[i-1] == b[j]，因此需要判断一下 b[i-1] 是否等于 b[j]
		if b[i-1] == b[j]{
			j++
		}
		next[i] = j
	}
	return next
}

KMP的平均时间复杂度为O(m+n)，空间复杂度O(m)，m是模式串长度。

更多内容请关注微信公众号