更多优质内容
请关注公众号
请关注公众号
回溯算法本质是一种对决策树（是一个多叉树）通过深度优先遍历列出问题所有情况的算法，也就是所谓的暴力解。
回溯算法适用于全排列问题和暴力解问题（如果想要得到一个问题的最优解，但想不到复杂度更优的思路，可以使用暴力解列出所有可能的解，并从中得到最优解）。
在之前介绍图算法中，图的深度优先遍历所有节点本质上也是一种回溯算法，从逻辑上，对图的深度优先遍历时避免遍历重复节点，其本质也是对决策树的深度遍历。
重要的事情说3遍：
回溯算法本质是对决策树进行深度优先遍历。
回溯算法本质是对决策树进行深度优先遍历。
回溯算法本质是对决策树进行深度优先遍历。
决策树的特征：
0、决策树是一个多叉树，非叶子节点至少有1个子节点。
1、决策树的某个节点下的所有子节点代表当前子问题下所有可以选择的情况。
2、对于一个有n个叶子节点的决策树，从根节点到达所有叶子节点的路径有n条（从根节点到达某一叶子节点的路径是唯一的），则原问题就有n个解。
3、深度遍历决策树的所有叶子节点（即回溯算法、暴力解算法）的复杂度为O(N!)阶乘级别，可以通过剪枝的方式优化回溯算法复杂度，对越高层的节点进行剪枝，剪枝数量越多，优化程度越明显。但不管怎么优化，回溯算法的时间复杂度都不可能低于 O(N!)。
使用回溯算法时只需要思考 3 个问题：
1、记录当前路径：也就是已经做出的选择（即已经遍历过的树节点）。
2、选择列表：当前子问题情况下可供做出的选择（当前树节点的所有子节点就是当前选择列表中的所有选择）。
3、结束条件：到达决策树底层（即叶子节点），无法再做选择时，就满足结束条件（此时需要回溯到上一个节点，寻找其他路径）。
回溯算法的框架：
result = []
def backtrack(当前路径, 选择列表): # 当前路径具体是指某条路径上已经经过的节点
if 满足结束条件:
result.add(当前路径) // 一个完整路径就是result的一个解
return
for 选择 in 选择列表:
make_decision(选择) // 前序遍历需要做选择
backtrack(当前路径, 选择列表)
cancel(选择) // 后序遍历需要撤销选择
def make_decision(选择):
将选择放入当前路径
def cancel(选择):
将选择从当前路径弹出
其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」。
for循环本质是对树的同一层节点的水平遍历，backtrack递归是树节点的深度遍历。
虽然回溯算法就是暴力穷举，但穷举也分聪明的穷举方式和低效的穷举方式，关键看以怎样的「视角」进行穷举。
通俗来说，我们应该尽量「少量多次」，就是说宁可多做几次选择（树的高度决定选择的次数），也不要在单次选择给出太大的选择空间（即宁愿树的高度大一点，而每层的节点少一点，也不要层数少但每层的节点多）；宁可「二选一」选k次，也不要 「k选一」选一次。这句话说的就是要尽可能剪枝。
在解题之前根据题意画出决策树对使用回溯算法解题有很大帮助。
下面通过几道力扣的题目来理解决策树和回溯算法。
力扣46. 全排列。给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
根据题意画出决策树：
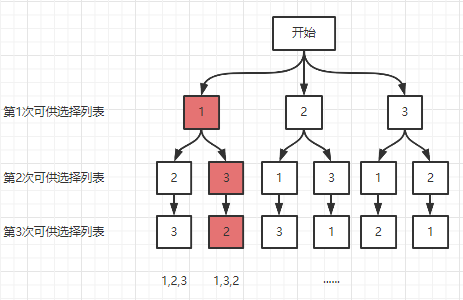
决策树的每一层都是一次决策机会，每一次决策机会都可以从该层的所有节点中选择一个符合条件节点往下层深入。
这棵决策树所有从根节点到达所有叶子节点的路径就是全排列的结果。
func permute(nums []int) [][]int {
if len(nums) == 1{
return [][]int{{nums[0]}}
}
if len(nums) == 0{
return [][]int{}
}
leng := len(nums)
path := make([]int, 0) // 已选择路径
choice := make([]bool, leng) // 判断某一个元素是否已经被选择过
res := make([][]int, 0)
var solutionPermute func()
solutionPermute = func (){
if len(path) == leng{
res = append(res, []int{})
res[len(res)-1] = append(res[len(res)-1], path...)
return
}
for i, num := range(nums){
if choice[i]{
continue
}
choice[i] = true
path = append(path, num)
solutionPermute()
choice[i] = false
path = path[:len(path)-1]
}
}
solutionPermute()
return res
}力扣78. 子集
给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
这道题可以分为多个决策树，假设nums的长度为n，则每个子集可能的长度为 0 ~ n 。那么某个决策树 tree(k) 的含义是：子集元素个数为 k 的情况下，所有可能的子集。这样，获取一个子集需要做k次选择，因此该树的层数为k。
如下图：nums = [1,2,3,4]，k = 3，这个树表示长度为3的所有子集，可以画成
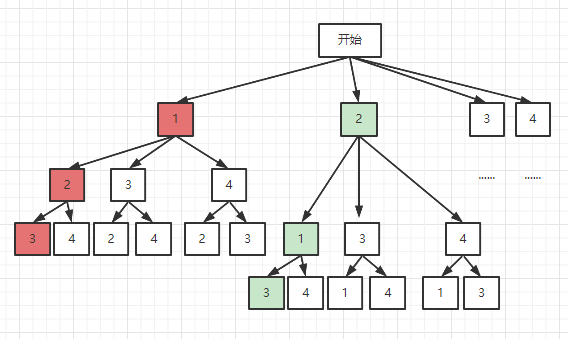
但是有一个问题，遍历整棵树的时候肯定会出现重复的子集，例如图中红色和绿色的子集是相同的：[1,2,3], [2,1,3]（题目规定两个子集内的元素相同，即使顺序不同，这两个子集也算重复）。
又例如下图中红色和蓝色的也是重复子集：[1,2,3]，[1,3,2]。
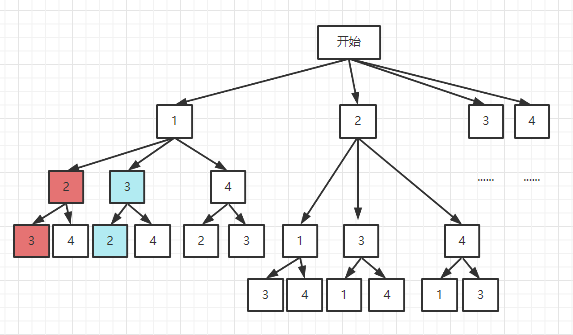
此时需要对这个树进行剪枝，剪枝的目的是为了提出重复的子集，同时顺便减小每层的可供的选择个数。
经过观察，每一个相同的子集会有多种顺序，但我只取一种顺序即可，而且我只取升序的那种顺序：[1,2,3]，[1,3,2]，[2,1,3]，[2,3,1]，我只选[1,2,3]即可。既然规定了只取升序的那个子集作为目标子集就好办了，每一层选择某个数 x 作为开头，那么下一层的选择就只能选比x大的节点，比x小的节点要被剪枝。为此我们需要对nums先进行升序排序，这样树的每一层才会是有序的。
剪枝后的结果如下（虚线是剪掉的分支）：
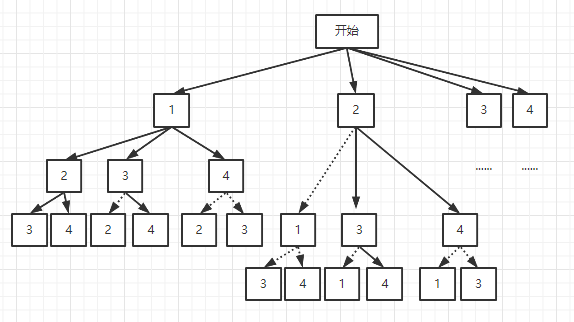
代码：
func subsets(nums []int) [][]int {
allSet := [][]int{{}}
n := len(nums)
var backtrack func(curLen, subsetLen, start int)
var subset []int
sort.Ints(nums)
backtrack = func(curLen, subsetLen, start int){ // curLen是某个子集当前的长度，subsetLen是规定要到达的子集的长度,start表示只从nums[start:]的范围选
if curLen == subsetLen{
allSetLastIdx := len(allSet)
allSet = append(allSet, make([]int, 0, subsetLen))
allSet[allSetLastIdx] = append(allSet[allSetLastIdx], subset...)
return
}
for i:=start; i<len(nums); i++{
subset = append(subset, nums[i])
backtrack(len(subset), subsetLen, i+1)
subset = subset[:len(subset)-1]
}
}
for i:=1; i <= n-1; i++{ // 遍历n个决策树
subset = make([]int, 0, i) // subset是长度为i下的某个具体子集
backtrack(0, i, 0)
}
allSet = append(allSet, nums)
return allSet
}