本节介绍有关Python数值运算的numpy模块,进而为后面章节的统计运算和机器学习打下基础,具体内容有: 数组的创建与操作; 数组的基本数学运算; 常用数学和统计函数; 线性代数的求解; 伪随机数的创建。
1.数组的创建与操作
2. 数组的基本数学运算
import numpy as np
arr_txt = np.genfromtxt("./stu_socre.txt",delimiter="\t",skip_header=1)
print(arr_txt)
a1,a2,a3 = arr_txt[:,0],arr_txt[:,1],arr_txt[:,2]
print(a3)
print(a1+a2+a3)
print(np.add(a1,a2))
arr1 = np.array([[2,6,3],[10,1,7],[9,4,5]])
arr2 = np.array([[2,2,2],[3,3,3],[4,4,4]])
print(arr1 % arr2)
print(arr1 // arr2)
print(arr1 ** arr2)
print(arr1[arr1>arr2])
arr3 = np.array([8,40,29,5,26,77,100])
print(arr3[arr3>50])
print(arr1[np.where(arr1>7)])
print(np.where(arr1>7,5,arr1))
print(np.where(arr1>7,5,0))
arr4 = np.arange(60).reshape(5,4,3)
arr5 = np.arange(12).reshape(4,3)
print(arr4+arr5)
arr6 = np.arange(4).reshape(4,1)
print(arr4+arr6)
arr7 = np.arange(3).reshape(1,3)
print(arr4+arr7)
arr8 = arr7.flatten()
print(arr4+arr8)


3.线性代数运算和伪随机函数
import numpy as np
from numpy import linalg
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
arr1 = np.arange(30).reshape(5,6)
print(np.sum(arr1))
print(np.sum(arr1,axis=0))
print(np.sum(arr1,axis=1))
arr2 = np.dot(np.array([0,1,2]),np.array([3,4,5]))
print(arr2)
arr3=np.arange(12).reshape(3,4)
arr4=np.arange(100,112).reshape(4,3)
print(arr3)
print("\r\n")
print(arr4)
print(np.dot(arr3,arr4))
arr5 = np.arange(16).reshape(4,-1)
print(np.diag(arr5))
print(np.diag(np.array([1,2,3])))
arr6 = np.array([[1,2,5],[3,6,8],[4,7,9]])
print(linalg.eig(arr6))
x = np.array([[1,1,4,3],[1,2,7,6],[1,2,6,6],[1,3,8,7],[1,2,5,8],[1,3,7,5],[1,6,10,12],[1,5,7,7],[1,6,3,4],[1,5,7,8]])
y = np.array([3.2,3.8,3.7,4.3,4.4,5.2,6.7,4.8,4.2,5.1])
x_trans_x_inverse = linalg.inv(np.dot(np.transpose(x),x))
beta = np.dot(np.dot(x_trans_x_inverse,np.transpose(x)),y)
print(beta)
A = np.array([[3,2,1],[2,3,1],[1,2,3]])
b = np.array([39,34,26])
X = np.linalg.solve(A,b)
print(X)
arr7 = np.array([1,3,5,7,9,10,-12])
print(linalg.norm(arr7,ord=1))
print(linalg.norm(arr7,ord=2))
print(linalg.norm(arr7,ord=np.inf))
np.random.seed(1234)
rn1 = np.random.normal(loc=0,scale=1.0,size=1000)
rn2 = np.random.normal(loc=0,scale=2.0,size=1000)
rn3 = np.random.normal(loc=2,scale=3.0,size=1000)
rn4 = np.random.normal(loc=5,scale=3.0,size=1000)
plt.style.use("ggplot")
sns.distplot(rn1,kde=False,hist=False,fit=stats.norm,fit_kws={'color':'black',"label":'u=0,s=1',"linestyle":'-'})
sns.distplot(rn2,kde=False,hist=False,fit=stats.norm,fit_kws={'color':'red',"label":'u=0,s=2',"linestyle":'--'})
sns.distplot(rn3,kde=False,hist=False,fit=stats.norm,fit_kws={'color':'blue',"label":'u=2,s=3',"linestyle":':'})
sns.distplot(rn4,kde=False,hist=False,fit=stats.norm,fit_kws={'color':'purple',"label":'u=5,s=3',"linestyle":'-.'})
plt.legend()
plt.show()


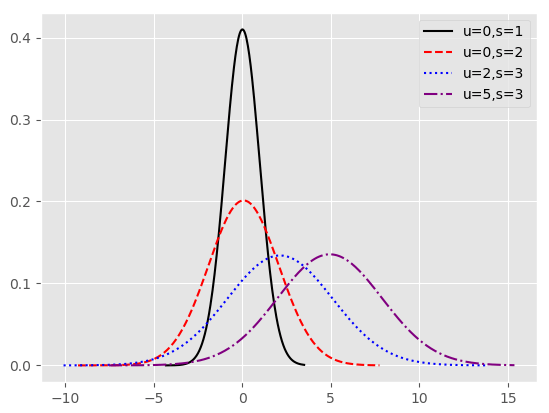
正态分布随机数概率分布图
更多内容请关注微信公众号




