上一节在介绍BST时说道BST可能发生因插入顺序而产生的的退化为单链表的问题，这会使得BST的查询复杂度退化为O(n)，为了解决这个问题，具有自平衡树就出现了。其中 AVL树 是最基础的一款自平衡树，其他各种各样的自平衡树都是在AVL的基础上改进的。

 

· AVL如何实现自平衡

AVL树是在BST的基础上对每个节点设置一个“平衡因子”信息表示其左右子树的高度差，每次插入或者删除一个节点时会根据节点的平衡因子调整树，使得树的左右子树高度不会超过1从而达到平衡，平衡因子的绝对值在[-1,1]之间。每个节点不记录平衡因子属性，而是记录高度属性，一个节点的平衡因子通过其左右子节点的高度计算得出。下图为每个节点和它的平衡因子：

 

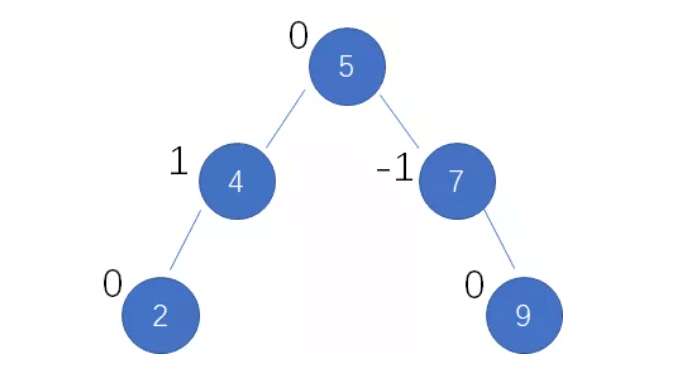
AVL的定义如下：

// 二叉平衡树节点
type AVL struct{
	Left *AVL		// 左子树
	Right *AVL		// 右子树
	Val int
	Height int		// 节点高度
}

func InitAVL(val int) *AVL{
	return &AVL{Val: val, Height: 1}
}

// 中序遍历
func InOrderTravelAVL(root *AVL){
	if root == nil {
		return
	}
	InOrderTravelAVL(root.Left)
	fmt.Print(root.Val, root.Height)
	fmt.Print(" | ")
	InOrderTravelAVL(root.Right)
}

// 二叉平衡树
type AvlTree struct{
	root *AVL
}

func InitAvlTree() *AvlTree{
	return &AvlTree{}
}

// 中序遍历
func (this *AvlTree) InOrderTravel(){
	if this == nil{
		return
	}
	InOrderTravelAVL(this.root)
}

 

·什么时候平衡左右子树

当插入和删除一个节点后，树的相关节点的平衡因子会发生改变。如果插入和删除导致某些节点平衡因子的绝对值超过1（即 平衡因子 ∉[-1, 0, 1]）时，这些节点都要做出平衡使其平衡因子小于等于1。

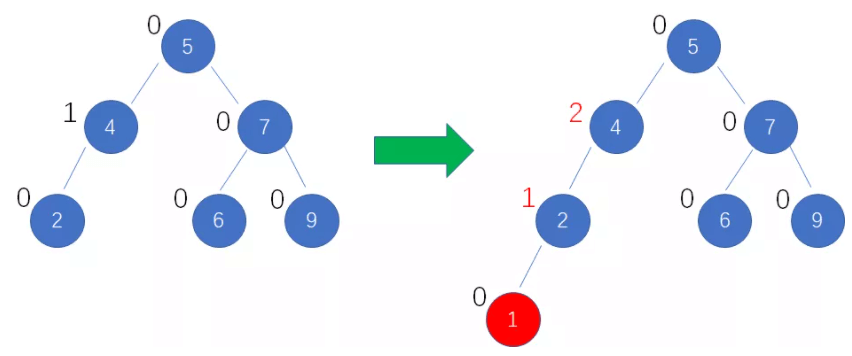
·如何平衡

“平衡”的具体做法包括 查看某个节点是否平衡（计算其平衡因子是否∈[-1, 1]） + 左旋和右旋 + 更新旋转后的节点及其祖先节点的高度。

 

1. 节点是否平衡

需要计算该节点的平衡因子是否∈[-1, 1]，而一个节点A的平衡因子 = A.Left的高度 - A.Right的高度。

// 计算节点平衡因子
func getBalance(node *AVL) int{
	return getLeftHeight(node) - getRightHeight(node)
}

// 获取某节点（不含该节点本身）左边的高度
func getLeftHeight(node *AVL) int{
	if node.Left == nil{
		return 0
	}
	return node.Left.Height
}

// 获取某节点（不含该节点本身）左边的高度
func getRightHeight(node *AVL) int{
	if node.Right == nil{
		return 0
	}
	return node.Right.Height
}

 

2. 更新节点高度

一个节点A的高度 = Max(A.Left的高度, A.Right的高度) + 1

// 更新一个节点node的高度
func updateHeight(node *AVL){
	if node == nil{
		return
	}
	leftHeight := getLeftHeight(node)
	rightHeight := getRightHeight(node)

	var Longer int
	if leftHeight >= rightHeight{
		Longer = leftHeight
	}else{
		Longer = rightHeight
	}
	node.Height = Longer + 1
}

 

3. 左旋和右旋

左旋

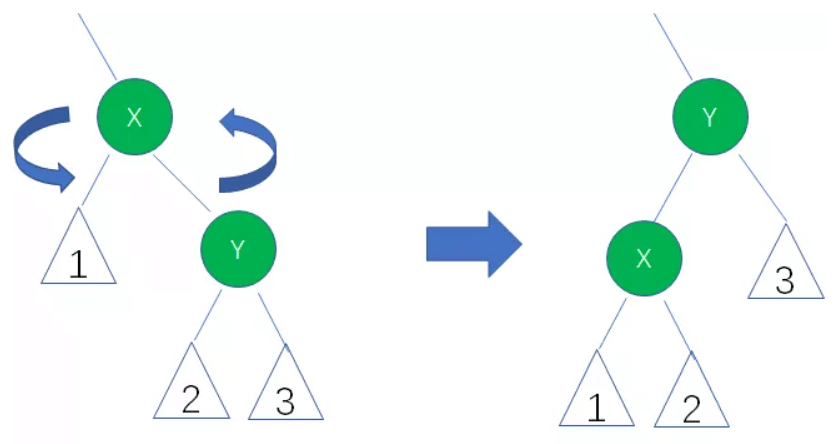
右旋

 

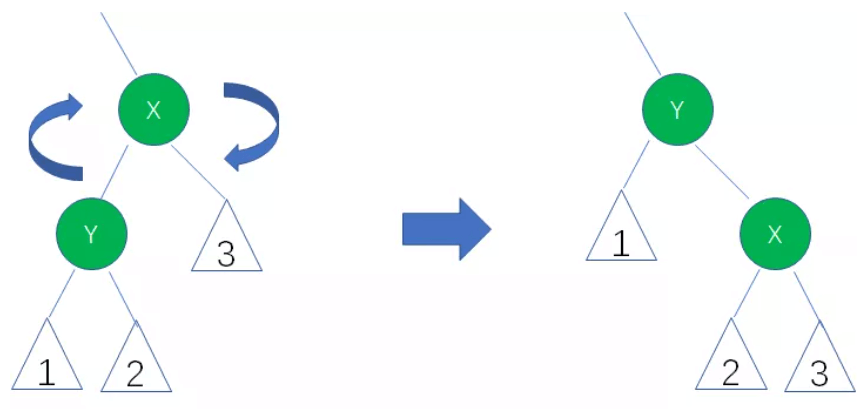
什么情况下用左旋，什么情况下用右旋。

在所有实际情况中，只会出现以下4中情况，只需对这4中情况一一判断和处理即可。图中的小三角表示子树。

A. 左左局面（LL）使用右旋

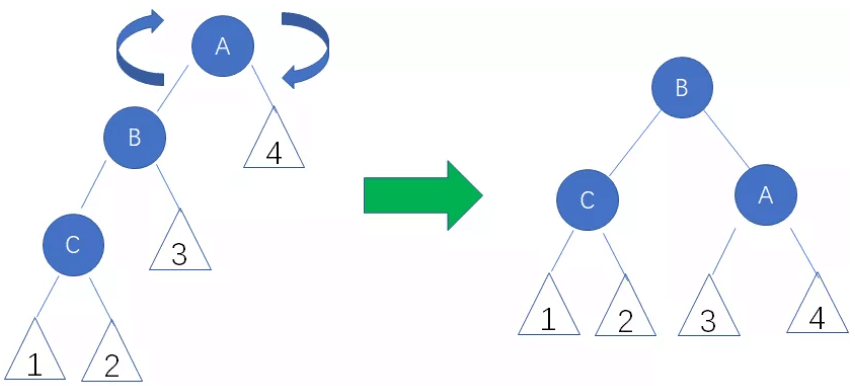
// 左左局面旋转(右旋）
func llRotate(node *AVL) *AVL{	// 返回旋转之后位于node位置的新节点
	leftNode := node.Left
	node.Left = leftNode.Right
	leftNode.Right = node
	updateHeight(node)		// 更新节点高度时，必须先更新低层节点，后更新高层节点，因为高层节点的Height是根据低层节点的Height计算的
	updateHeight(leftNode)
	return leftNode
}

 

B. 右右局面（RR）要左旋

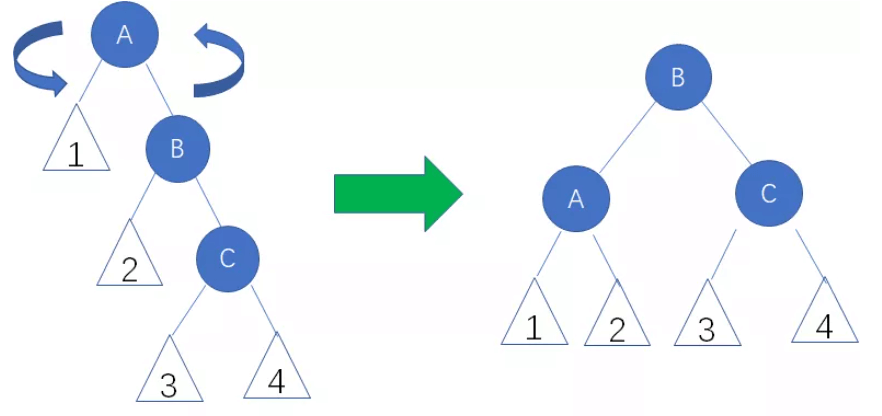
// 右右局面旋转(左旋）
func rrRotate(node *AVL) *AVL{	// 返回旋转之后位于node位置的新节点
	rightNode := node.Right
	node.Right = rightNode.Left
	rightNode.Left = node
	updateHeight(node)
	updateHeight(rightNode)
	return rightNode
}

 

C. 左右局面（LR）要先对B左旋变成LL局面，再对A右旋

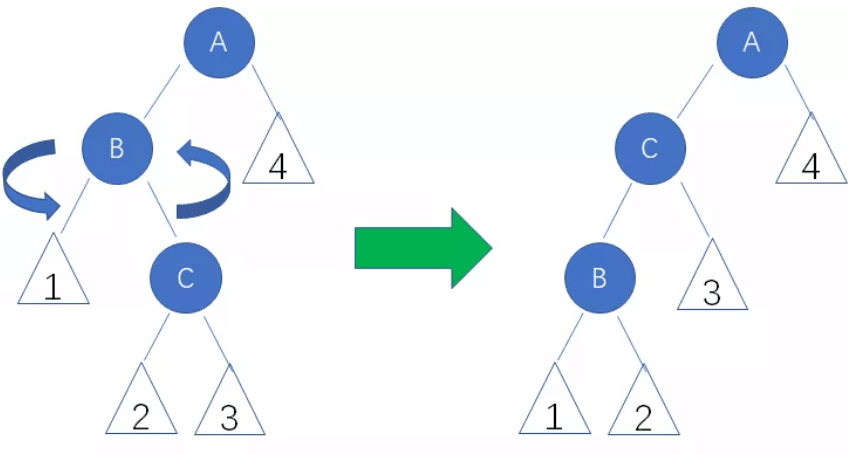
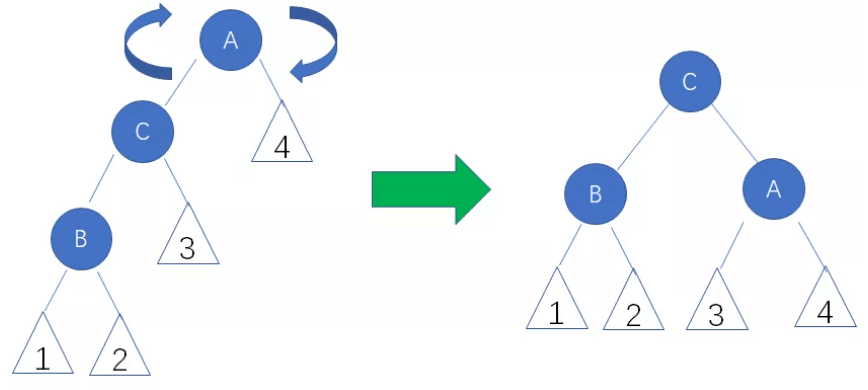
// 左右局面旋转（先左旋再右旋）
func lrRotate(node *AVL) *AVL{	// 返回旋转之后位于node位置的新节点
	node.Left = rrRotate(node.Left)	// 记得把 node的Left指针 指向旋转后的新节点
	return llRotate(node)
}

 

D. 右左局面（RL）要先对B左旋，再对A右旋

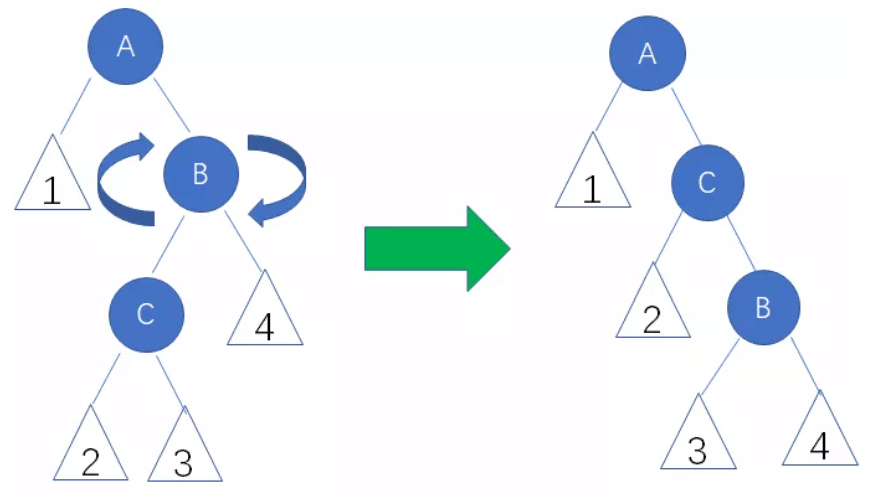
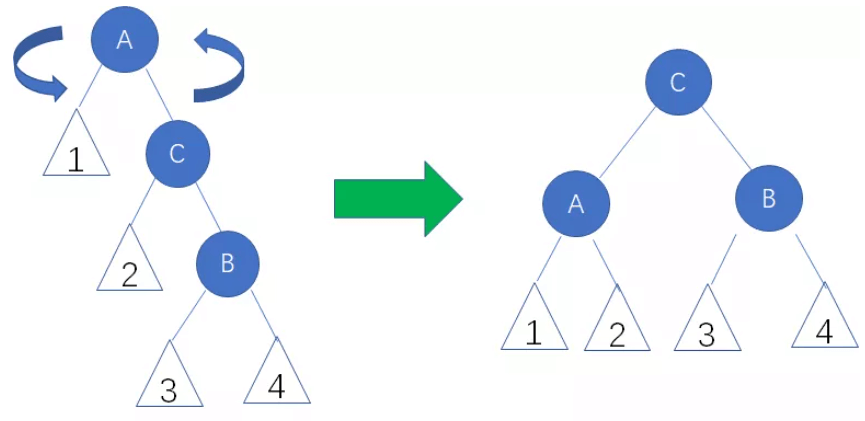
// 右左局面旋转
func rlRotate(node *AVL) *AVL{	// 返回旋转之后位于node位置的新节点
	node.Right = llRotate(node.Right)
	return rrRotate(node)
}

需要注意的是，旋转节点会导致节点高度发生变化，因此在旋转过程中需要更新旋转节点的高度（llRotate方法中调用了updateHeight方法更新了旋转节点的高度）。

 

·关于插入和删除的细节

1、高度概念的引入 和 某个节点的平衡因子如何计算

我们不直接记录每个节点的“平衡因子”，而是记录每个节点的高度，叶子节点的高度为1。父节点的高度 = 左右子节点中高度最大的高度+1。

 

节点高度的含义是以该节点作为起始节点到其尾部节点的最长的一条链表的长度。

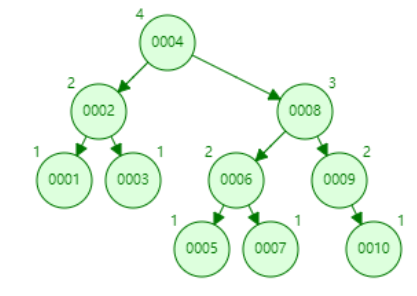
如图所示，0004节点的高度为4，表示以0004作为起始节点的最长的一条单链表（0004 - 0008 - 0009 - 0010）的长度。

一个节点A的平衡因子 = 左子节点的高度（A左侧最长链表的长度） - 右子节点的高度（A右侧最长链表的长度）

 

2、后续遍历和高度的修改

插入和删除某个节点A需要先找到A所在的位置，这个查找过程是一个单链表（二叉树的其中一条分支）的遍历过程，并且需要在插入或者删除之后，修改这个单链表所有节点的高度，由于我们是在插入或者删除之后才能重新确认这条分支的每个节点的高度，因此这是一个单链表的后序遍历（也就是对链表的子节点修改高度之后再对父节点修改高度，因为父节点的高度是基于子节点的高度计算的），会使用到递归。每次递归只需更新本节点的高度即可。

 

需要注意的是，旋转某个节点A的时候，会更新A和A的所有祖先节点的高度，但是无需更新A的子树节点的高度，旋转是不会影响子树所有节点的高度的，因为高度的计算是一个自底向上的过程而非自顶向下，改变下层节点的高度会影响上层节点的高度，反之则不会。例如上图中展示的4种旋转情况，凡是小三角里面的节点，他们的高度都不会变。

 

 

下面是自动平衡、查找、删除、插入的代码：

自动平衡

// 自动平衡(平衡完之后会自动修改node的高度，返回旋转后的node)
func autoBalance(node *AVL) *AVL{
	if node == nil {
		return nil
	}
	balance := getBalance(node)
	if balance > 1{ // 左左或者左右局面
		if getLeftHeight(node.Left) > getRightHeight(node.Left){	// 左左局面
			node = llRotate(node)
		}else{	// 左右局面；else的局面只可能是 getLeftHeight(node.Left) < getRightHeight(node.Left)，不可能是 ==，如果是==的话那node的balance就不可能大于1或者小于-1
			node =  lrRotate(node)
		}
	}else if balance < -1{
		if getLeftHeight(node.Right) > getRightHeight(node.Right){	// 右左局面
			node =  rlRotate(node)
		}else{	//右右局面
			node =  rrRotate(node)
		}
	}
	return node
}

 

查找

// 查找
func (this *AvlTree) Find(target int) *AVL{
	if this == nil{
		return nil
	}

	targetNode := this.root
	for targetNode != nil{
		if targetNode.Val > target{
			targetNode = targetNode.Left
		}else if targetNode.Val < target{
			targetNode = targetNode.Right
		}else{
			return targetNode
		}
	}
	return nil
}

 

插入

// 插入
func (this *AvlTree) AVLInsert(target int) *AVL{	// 返回插入的节点
	if this.root == nil{
		this.root = InitAVL(target)
		return this.root
	}

	var newNode *AVL
	this.root, newNode = this.avlInsertHelper(this.root, target)
	return newNode
}

// 往node这个树里面添加target
func (this *AvlTree) avlInsertHelper(node *AVL, target int)  (*AVL, *AVL){	// 返回根节点和插入的节点
	var newNode *AVL
	if node == nil{	// 到达叶子节点(不会出现最顶端根节点为nil的情况，该情况已经被AVLInsert拦截了)
		newNode = InitAVL(target)
		return newNode, newNode
	}

	if node.Val >= target{
		node.Left, newNode = this.avlInsertHelper(node.Left, target)
	}else{
		node.Right, newNode = this.avlInsertHelper(node.Right, target)
	}
	node = autoBalance(node)	// 自动平衡当前节点，旋转完之后位于原本node位置的节点可能是新节点
	updateHeight(node)		// 更新当前节点的高度，虽然在 autoBalance 内部已经更新过一次高度。但是autoBalance内的更新高度是因为旋转而更新高度，如果node并没有旋转，此时我们就要在autoBalance外手动给tree更新高度
	return node, newNode
}

 

删除

// 删除
func (this *AvlTree) AVLDelete(target int) (delSucc bool){
	if this.root == nil{
		return false
	}
	this.root, delSucc = this.avlDeleteHelper(this.root, target)
	return delSucc
}

// 往node这个树删除目标值target
func (this *AvlTree) avlDeleteHelper(node *AVL, target int) (*AVL,bool){	// 返回删除后的node节点 和 删除结果
	if node == nil{
		return nil, false
	}

	var delSucc bool
	if node.Val > target{
		node.Left, delSucc = this.avlDeleteHelper(node.Left, target)
	}else if node.Val < target{
		node.Right, delSucc = this.avlDeleteHelper(node.Right, target)
	}else{
		if node.Left != nil && node.Right != nil{	// 当node有左右子树时，需要从较高的子树那里获取后继节点（左子树的最大节点或右子树的最小节点），这样可以减少平衡的次数
			var succNode *AVL
			if getLeftHeight(node) >= getRightHeight(node){
				succNode = this.FindMaxNode(node.Left)
				node.Val = succNode.Val
				node.Left, _ = this.avlDeleteHelper(node.Left, succNode.Val)
			}else{
				succNode = this.FindMinNode(node.Right)
				node.Val = succNode.Val
				node.Right, _ = this.avlDeleteHelper(node.Right, succNode.Val)
			}
		}else{	// 包含BST删除的2种情况：node有单个子节点或者无子节点
			if node.Left != nil{	// 当node有左节点
				node = node.Left
			}else{	// 当node有右节点或者左右节点都无
				node = node.Right
			}
		}
		delSucc = true
	}
	node = autoBalance(node)
	updateHeight(node)
	return node, delSucc
}

// 寻找 node 下最大的节点
func (this *AvlTree) FindMaxNode(node *AVL) *AVL{
	if node == nil{
		return nil
	}

	target := node
	for target.Right != nil{
		target = target.Right
	}
	return target
}

// 寻找 node 下最小的节点
func (this *AvlTree) FindMinNode(node *AVL) *AVL{
	if node == nil{
		return nil
	}

	target := node
	for target.Left != nil{
		target = target.Left
	}
	return target
}

 

 

·优点和缺点

AVL树维护的是绝对的平衡，这样查找效率相比于其他自平衡的树高，但为了绝对平衡，AVL的插入和删除（复杂度是O(logn)）的成本也比BST以及其他具有自平衡的树高。因为AVL每一次插入和删除一个节点P都要更新P和P所有祖先节点的高度。

 

相比之下，另一种非常常用的自平衡的二叉查找树——红黑树，它在保持平衡的要求上就没AVL那么严格，插入和删除的性能比AVL高。