更多优质内容
请关注公众号
请关注公众号
拓扑排序是针对有向无环图的一种广度优先遍历顶点的算法，可以将图中所有顶点按照要求的先后顺序排序。当然，拓扑排序本质不是一种排序算法，而是一种遍历图的算法。
在如果存在顶点 u 和顶点 v，要想到达顶点 v，则必须要到达顶点 u 。那么在拓扑排序中，顶点 u 必须处于顶点 v 的前面。
课程表的规划是拓扑排序的经典应用。
· 拓扑排序算法原理
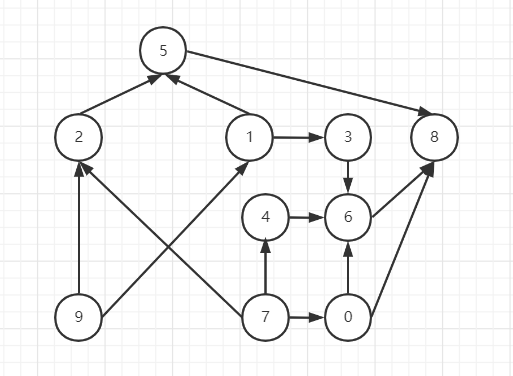
图中的每个顶点都有入度和出度两个属性，入度是指该顶点被多少个顶点指向，出度指该顶点指向了多少个顶点。
1、创建一个队列，队列里存放所有入度为0的节点。
2、每次从队列中弹出一个节点A，记录为已访问。将A的未访问过的相邻节点的入度-1（但这些节点未访问），并将新的入度为0的节点放入队列。
3、重复步骤2，直到队列为空。
不能完成拓扑排序的情况：
1、如果初始状态下，所有节点的入度都为0，说明图中所有顶点都成环，无法完成拓扑排序；
2、如果队列为空后，图中仍存在未访问的节点，说明图中部分顶点成环，无法完成拓扑排序。
拓扑算法本质是广度优先遍历 + 贪心算法，假设最终解为res数组，存储拓扑排序后顶点的顺序。每一个局部最优解是入度为0的顶点，优先访问掉这些顶点放入res中，并生成新的入度为0的未访问顶点，再进入下一个局部状态。
代码实现如下：
// 拓扑排序, 参数是邻接表形式，要学习 g[i] 的课程，必须先学习 i
func KahnSort(g [][]int) []int{
queue := list.New() // 存储入度为0的队列
level := make(map[int]int) // 存储所有顶点的入度，可理解为学习某课程的难度
visited := make(map[int]struct{}) // 存储所有已访问过的节点
res := make([]int, 0, len(g))
// 统计所有顶点的入度
for vext, neibors := range(g){
if _, ok := level[vext]; !ok{
level[vext] = 0
}
for _, neibor := range(neibors){
level[neibor] += 1
}
}
for vext, lv := range(level){
if lv == 0{
queue.PushBack(vext)
}
}
for queue.Len() > 0{
node := queue.Front()
queue.Remove(node)
vext := node.Value.(int)
visited[vext] = struct{}{}
res = append(res, vext)
for _, neibor := range(g[vext]){
if _, ok := visited[neibor]; ok{
continue
}
level[neibor]-- // 访问neibor顶点的困难-1
if level[neibor] == 0{ // 如果访问neibor的难度为0则假如队列
queue.PushBack(neibor)
}
}
}
// 判断是否存在还没有访问的顶点
if len(visited) < len(g){
return []int{}
}
return res
}
测试用例如下：
func TestKahnSort(t *testing.T){
g := [][]int{
{6,8},
{3, 5},
{5},
{6},
{6},
{8},
{8},
{2,4,0},
{},
{1,2},
}
fmt.Println(KahnSort(g)) // [7 9 4 0 1 2 3 5 6 8]
}