请关注公众号


先抛出一个问题:给出两个字符串A和B,如何判断B是否为A的子串并返回B在A中第一次出现的位置?
A是主串,B是模式串。
· BF算法(暴力法)
使用两个指针 j 和 j 指向 主串和模式串的第一个字符,遍历主串。
每遍历主串的一个字符,都要与B进行一轮字符匹配,每一轮字符匹配如下:
如果 A[i] != B[j],则 i++,进行下一轮字符匹配;
如果 A[i] == B[j],则创建第三个指针 k = i,然后 k++ 且 j++,继续比较 A[k] 和 B[j],如果不相等,则 j 置为0,进行下一轮字符匹配。
在某一轮字符匹配中,当 j 达到模式串B 的len(B)位置,说明主串包含模式串,当前 i 就是B在A的开始位置。
假设主串长度为m,子串长度为n,则最多可能要进行m轮字符匹配,每轮字符匹配最多可能比较n的长度,因此BF算法的复杂度为 O(mn)。
在某些极端情况,BF算法的效率会很低(O(nm)),例如:

每一轮字符匹配,模式串的前三个字符a都和主串中的字符相匹配,一直检查到模式串最后一个字符b,才发现不匹配:

· RK算法
该算法的思想是:判断两个字符串是否是相同的字符串,不必靠比较两个字符串的所有字符,而是靠比较两个字符串的哈希值。
计算一个字符串的哈希值有2种方法:
A 按位相加
把a当做1,b当做2,c当做3......然后把字符串的所有字符相加,相加结果就是它的hashcode。
bce = 2 + 3 + 5 = 10
这个算法虽然简单,却很可能产生hash冲突,比如bce、bec、cbe的hashcode是一样的。因此如果 hash(A) == hash(B),还需要比较A和B的逐个字节才能确定A == B。
B 转为26进制
字符串只包含26个小写字母,那么我们可以把每一个字符串当成一个26进制数来计算。
bce = 2*(26^2) + 3*26 + 5 = 1435
好处是大幅减少了hash冲突的可能,缺点是计算量较大(因为涉及到乘法和指数运算),而且有可能出现超出整型范围的情况,需要对计算结果进行取模。
RK算法的过程(使用按位相加法):
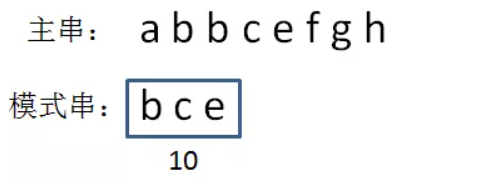
1、一开始需要指针 i 和 j 指向主串A和模式串B的开头。假设 A 的长度为m,B的长度为n,则需要进行最多 m 轮的字符串匹配。
2、每一轮字符匹配过程如下
计算 A[i:i+n] 的哈希值 h(a) 与 B 的哈希值 h(b) 比较。如果不相等则 i++,进入下一轮字符匹配;如果相等则 让 A[i:i+n] 与 b 逐个字符比较,比较失败则进入下一轮字符匹配,成功则返回。
RK的复杂度:第一次计算 A[i:i+n]的哈希值其复杂度为 O(n),因为需要累加 A[i:i+n] 中所有字符的相位值,但是之后每轮字符匹配计算 A[i:i+n] 的哈希值为 O(1),因为每一个A子串的hash都可以由上一个子串进行简单增量计算:
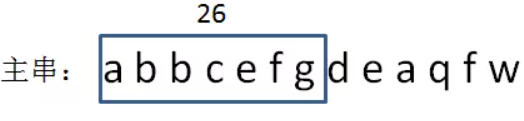
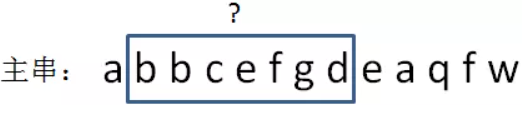
新hashcode = 旧hashcode - 1 + 4 = 26-1+4 = 29
RK算法需要进行 m 轮字符匹配, 每轮字符匹配复杂度为 O(1),但哈希值相同的那一轮需要逐字符比较,复杂度为O(n),因此总复杂度为 O(m+n)。
RK算法的缺点在于哈希冲突如果过多,每一次冲突都要进行逐字符比较,则复杂度退化为 O(mn)。
