· 动态规划概述

动态规划(Dynamic programming，简称 DP)不是某一种具体的算法，而是一种算法思想：若要求解一个给定问题，我们需要先解其子问题，再根据子问题的解得出原问题的解。

 

· 动态规划要点

1、首先动态规划问题的一般形式就是求最值。

2、因为要求最值，肯定要把所有可行的答案穷举出来，然后在其中找最值。所以求解动态规划的核心是穷举。

3、穷举的过程中可能存在重叠子问题，因此暴力穷举的话效率会极其低下，需要一个起到备忘录作用的DP表来记录所有穷举过的结果，避免重复计算。DP表不仅是一个备忘录，还是一个最终结果，是题目所需的解。

4、若要得到原问题的最优解，就需要在定义最优子结构的情况下先得到子问题最优解，因为原问题的最优解是建立在子问题最优解为基础的。

5、“如何定义子问题才能通过子问题的解得到原问题的解”这叫做定义最优子结构。如果定义子问题都定义错了，即使得到了子问题的最优解，也无法转为原问题的最优解。

定义最优子结构之后，“如何把求解原问题的解转为求解子问题的解”，这就涉及到状态转移方程，该方程能帮助我们把原问题转为子问题（如果定义的子结构不是最优的，或者说定义的子结构不对，那么得到的状态转移方程也是错误的）。

6、动态规划可以使用自底向上（迭代）或者自顶向下(递归)2种方式解决。使用自底向上（迭代）解题比用自顶向下(递归)的效率高，因为递归需要将函数使用到的临时变量压栈，占用空间更多，空间复杂度更高。

 

一个问题有什么「状态」，有什么「选择」，然后穷举，这就是动规的思路。

 

 

 

· 动态规划思想经典案例

 

斐波那契数列

题目如下：求n=20的斐波那契数列值。

 

斐波那契数列规律如下

           {

f(n) =         1, n∈{1,2}

                  f(n-1) + f(n-2), n > 2

             }

 

斐波那契数列代码实现：

func fib(n int) int {
    if n <= 2{
        return 1
    }
    return fib(n-1) + fib(n-2)    // 是一个二叉树的后序遍历
}

 

 

这种写法其问题在于复杂度太高，当n=20的时候，花费的时间很久。我们可以画出递归树分析一下其复杂度：

 

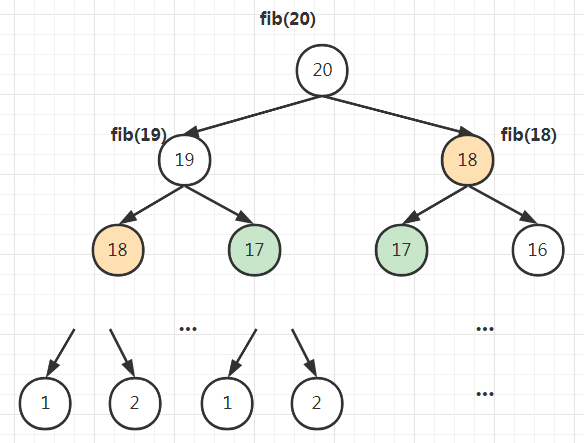
递归树的每个节点代表一次递归函数的调用。fib(n)的复杂度等于 递归次数 * 每次递归的复杂度。

fib(n)内部只有一个加法运算和 if判断，因此单次递归的复杂度为O(1)。

递归树的树高为 n = 20 层，共有约 2^0 + 2^1 + ... 2^19 = 2^20 - 1个节点，因此会发生2^n-1次递归调用。

综上，每次递归的复杂度为O(1)，共 2^n - 1次递归，因此总体复杂度为 O(2^n)。

这是一个指数级的复杂度。

 

下面介绍如何优化fib算法。

 

- 减少计算规模

我们可以看到递归树中有很多的重复节点（如下图标有颜色的节点），因此可以在递归的过程中使用一个dp表记住每次递归的结果，在下一次遇到相同的递归调用时，从dp表查结果直接返回即可。

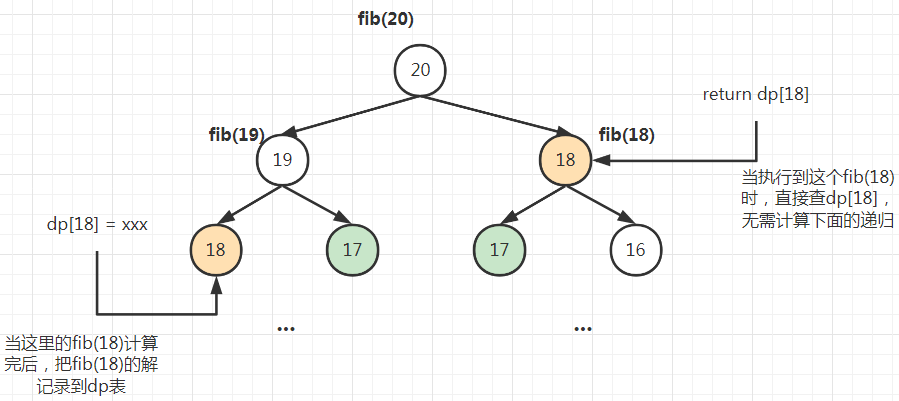
例如 左侧fib(18)的结果记录到dp表之后，右侧的fib(18)就不会重复计算，而是读取dp表内的结构，如此一来右侧fib(18)节点下的所有节点都无需计算，相当于剪枝。

 

代码实现如下：

var dp []int
func fib(n int) int {
    if n == 0{
        return 0
    }
    dp = make([]int, n+1)
    return fibHelper(n)
}
func fibHelper(n int) int{
    if n <= 2{
        dp[n] = 1
        return 1
    }
    if dp[n] != 0{
        return dp[n]
    }
    dp[n] = fibHelper(n-1) + fibHelper(n-2)
    return dp[n]
}

 

使用了dp表之后，dp[1]~dp[19]会在遍历递归树的最左侧路径时全部算好，整个递归树退化为一个链表（下图橙色部分所示），复杂度从O(2^n)优化为O(n)。

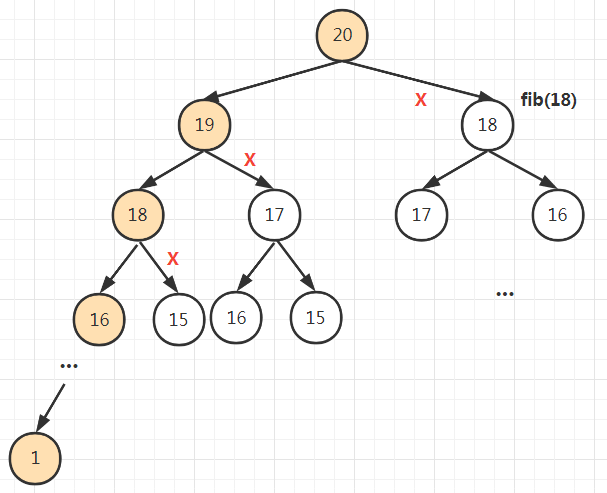
打了×的分支都不用重复计算。

带dp备忘录的递归算法把一棵存在巨量冗余的递归树通过「剪枝」，改造成了一个不存在冗余的链表，极大减少了子问题（即递归图中节点）的个数。

 

本题的解题方式是自顶向下（递归法）。

为什么叫自顶向下，因为上面代码的计算顺序是从fib(20)开始一直到fib(1)和fib(2)（从递归树中也可以直观的看出是自顶向下的遍历顺序）。

而dp表的构建是自底向上的，例如要知道dp[20]就要先知道dp[18]和dp[19]，要知道dp[18]就要先知道dp[17]。因此肯定要先得出递归树中所有子节点的dp值才能得到父节点的dp值，因此dp表的构建肯定是一个后序遍历，dp[k]的赋值是放在所有子节点递归之后的位置发生的。

此外DP表不仅是一个备忘录，也是一个结果表，是题目最终答案。

 

本题同样可以使用自底向上（迭代法）完成，实现从dp[1] -> dp[20]的顺序的构建dp表。

代码实现如下：

func fib(n int) int {
    if n == 0{
        return 0
    }
     if n <= 2{
        return 1
    }
    dp := make([]int, n+1)
    dp[1], dp[2] = 1,1
    for i:=3; i<=n; i++{
        dp[i] = dp[i-1] + dp[i-2]
    }
    return dp[n]
}

 

此外 fib(n)只需依靠n的前两个值计算，因此dp表无需记录1~n的所有结果集，只需记录最近的两个数n-1和n-2的结果即可。所以可以将dp表从一个一维数组压缩成2个普通变量，空间复杂度从O(n)优化为O(1)。

func fib(n int) int {
    if n == 0{
        return 0
    }
     if n <= 2{
        return 1
    }
    dp := make([]int, 2)
    dp[0], dp[1] = 1,1
    for i:=3; i<=n; i++{
        dp[0], dp[1] = dp[1], dp[0] + dp[1]
    }
    return dp[1]
}

 

 

“斐波那契数列”这个例子涉及到动态规划的2个关键点：状态转移方程和重叠子问题。

状态转移方程 就是当前问题fib(n) 和 子问题 fib(n-1) 的关系式：

    	{
f(n)   = 	    1,  n∈{1,2}
  		    f(n-1) + f(n-2), n > 2
    	}

 

重叠子问题 就是递归树中存在需要重复计算的树节点。可用dp表解决。

 

由于斐波那契数列没有涉及子问题最优解，因此严格来说，它不算一个动态规划问题，但是它用到了动规的思想。

 

 

下面我们再看一个经典的动态规划案例。

力扣322. 零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

动规题无论用迭代法还是递归法，关键是要把自变量（原问题）的规模不断缩小，找到本问题和子问题的关系（即状态转移方程）。

在本题中，以示例1为例，原问题 amount = 11 所需的最少硬币数 等于 amount = 11 - 1 = 10 或者 amount = 11 - 2 = 9 或者 amount = 11 - 5 = 6 这3个子问题所需的最少硬币数 + 1。

x的最优解 f(x) 等于 min(f(x-m)) + 1，其中 m 是coins中的某个面值，由于m有len(coins)种情况，所以我们需要找出 f(x-m)的最小值。

综上，得到状态转移方程为：

 

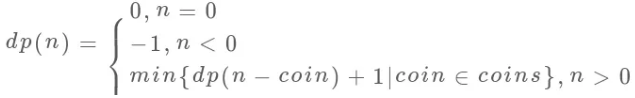
迭代法（python实现）：

class Solution:
    def coinChange(self, coins, amount):
        res = [0]  # res长度为amount+1
        coins.sort()
        for i in range(1, amount + 1):
            minNum = amount + 1  # 子问题中所需最少的硬币数
            for coin in coins:   # 子问题的个数为len(coins)
                smallerAmount = i - coin  # 子问题
                if smallerAmount < 0:
                    break
                if res[smallerAmount] != -1 and res[smallerAmount] < minNum:  # res[smallerAmount] == -1表示smallerAoumut这个子问题无解
                    minNum = res[smallerAmount]

            minNum = -1 if minNum == amount + 1 else (minNum + 1)
            res.append(minNum)
        return res[-1]

 

递归法（go实现）：

var dpCoins map[int]int
var coinsMap map[int]struct{}
func coinChange(coins []int, amount int) int {
   if amount == 0{
      return 0
   }
   sort.Ints(coins)
   dpCoins = make(map[int]int)
   coinsMap = make(map[int]struct{})
   for i:=0; i<len(coins); i++{
      coinsMap[coins[i]] = struct{}{}
   }
   return coinChangeHelper(coins, amount)
}

func coinChangeHelper(coins []int, amount int) int{
   if amount == 0{
      return 0
   }

   if coins[0] > amount{  // 如果amount小于最小面值
      dpCoins[amount] = -1
      return -1
   }

   if _, ok := coinsMap[amount]; ok{  // 如果amount不是某个面值
      dpCoins[amount] = 1
      return dpCoins[amount]
   }

   if _, ok := dpCoins[amount];ok{       // 不重复计算
      return dpCoins[amount]
   }

   dpCoins[amount] = -1
   for i:=len(coins) - 1; i >= 0; i--{
      if coins[i] < amount{
         tmp := coinChangeHelper(coins, amount - coins[i])
         if tmp != -1 && (dpCoins[amount] == -1 || dpCoins[amount] > tmp+1){       // 如果 amount - coins[i]的解为 -1 不代表 amount的解为-1，需要继续循环
            dpCoins[amount] = tmp + 1
         }
      }
   }
   return dpCoins[amount]
}

 

 

· 动态规划总结

动态规划问题的一般形式就是求最值。动态规划的解题思路本质是穷举（每次递归都在做选择），并去除重叠子问题。动规问题可以具象为一个递归树结构。

 

动规的3要素：

    最优子结构（即怎么定义dp表，或者怎么定义怎么解释递归函数）

    重叠子问题（用dp表记住已处理的情况，不重复处理相同的情况，相当于对递归树剪枝）

    状态转移方程（如何通过已处理过的问题得到当前问题的解，即当前问题和子问题之间的关系）

 

动规问题的2种解决方法：

    自底向上（迭代）

    自顶向下（递归）

 

动规问题的空间优化：

    对dp表状态压缩（二维数组压缩为一维，一维数组压缩为单个整数变量）

 

 

· 贪心算法

贪心算法的思想是：每一步都做出一个局部最优的选择，最终的结果就是全局最优。只要满足这个条件，就能使用贪心算法求解。

贪心算法本身是动态规划的一种，但性能更优于普通的动态规划，动态规划的复杂度为多项式级别，而贪心算法的复杂度可以在普通动态规划的基础上优化为线性级别。

 

解决一个问题需要多个步骤，每一个步骤有多种选择，这样的描述我们在「回溯算法」「动态规划」算法中都会看到。

贪心算法是动态规划的一种特殊情况，或者说是动规的优化。它和动规的相同点在于：规模较大的问题的解由规模较小的子问题的解组成。

区别在于：可以使用「贪心算法」来解决的问题，其「规模较大的问题的解」只由其中一个「规模较小的子问题的解」决定；

说简单点就是，动规问题每一步都有多个可能的选择，需要尝试多个可能的选择才能知道哪个选择更优；而贪心算法问题，每一步只有一个已知可以达到最优的选择，体现为递归树的一条分支。

 

贪心算法的经典问题可以参考 力扣-贪心算法问题集合

 

下面以一道题目为例。

435. 无重叠区间

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

注意:

可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。

 

这个问题在生活中的应用广泛，比如你今天有好几个活动，每个活动都可以用区间[start,end]表示开始和结束的时间，请问你今天最多能参加几个活动呢？

如果你学过算法，就可以比别人更高效地规划时间。

 

正确的思路其实很简单，可以分为以下三步：

1. 先将所有区间按照start升序排序，用两个指针p1和p2指向排序后的区间集合中的前两个区间，即 p1, p2 = 0, 1。区间p1是在当前所有区间中start 最小的区间。之所以排序是为了让start相近的区间聚集在一起，方便比较，start约相近的区间也可能发生相交。

2. 判断 p1 和 p2 这两个start临近的区间是否相交，如果相交则判断p1和p2他们谁的end比较大，删除那个end比较大的区间，因为end越大的区间，越可能和其他后面的区间（即start比x和y大的区间）重合，被删除的区间指针往后移。如果p1和p2不相交，则p1和p2都往后移。保持p2指针位于在p1指针的右边。

3. 重复判断p1和p2区间是否相交，直到p2到达最后一个区间。

 

代码实现

import "sort"

func eraseOverlapIntervals(intervals [][]int) int {
	newIntervals := _intervals(intervals)
	sort.Sort(newIntervals)
	deleteNum := 0
	p1, p2 := 0,1
	for  p2 < len(newIntervals){
		if _isCross(newIntervals[p1], newIntervals[p2]){
			if newIntervals[p1][1] > newIntervals[p2][1]{	// 删除p1所指的区间
				p1 = p2
                p2++
			}else{	// 删除p2所指的区间
				p2++
			}
			deleteNum++
		}else{
			p1 = p2
			p2++
		}
	}
	return deleteNum
}

// 判断两个区间是否相交
func _isCross(a1, a2 []int) bool{
	if a1[0] <= a2[0] && a1[1] > a2[0]{
		return true
	}

	if a1[0] >= a2[0] && a2[1] > a2[0]{
		return true
	}
	
	return false
}

type _intervals [][]int
func (this _intervals) Len() int {return len(this)}
func (this _intervals) Less(i, j int) bool {return this[i][0] < this[j][0]}
func (this _intervals) Swap(i, j int) {this[i], this[j] = this[j], this[i]}