图的定义

图是多个顶点（为和树区分，这里不叫节点，而叫顶点）通过多条边连接而成的网状结构，顶点之间呈多对多的关系（树节点之间则是呈一对多关系）。

树和图相比，树的节点之间是一对多的关系，并且存在父与子的层级关系；图的顶点之间是多对多的关系，并且所有顶点都是平等的。

 

 

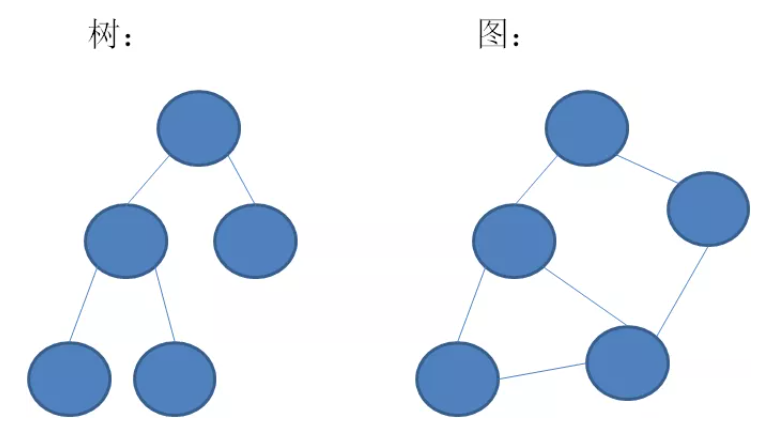
在图中，最基本的单元是顶点（vertex），相当于树中的节点。顶点之间的关联关系，被称为边（edge）。图的种类繁多，包括无向图、有向图、带权图等。

 

图的表示

图在内存中的存储方式多种多样，最主要包括：邻接矩阵、邻接表、逆邻接表和十字链表。

 

邻接矩阵是一个 n*n二维矩阵arr，对于拥有n个顶点的图，包含的连接数量（边的数量）最多为 n*(n-1)。

为什么连接数量为 n*(n-1)却需要n*n大小的矩阵呢？因为 n*(n-1)是每个顶点和其他顶点的关系，arr还描绘了每个顶点和自己的关系。

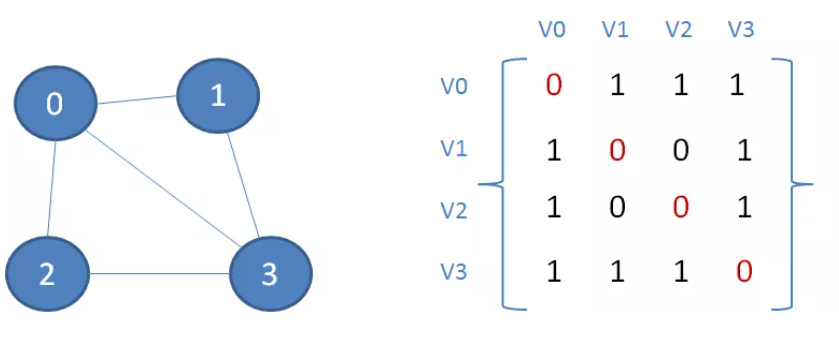
图中顶点0和顶点1之间有边关联，那么矩阵中的元素arr[0][1]与arr[1][0]的值就是1；顶点1和顶点2之间没有边关联，那么矩阵中的元素arr[1][2]与arr[2][1]的值就是0。

矩阵从左上到右下的一条对角线描述的就是顶点自己与自己的关联，其上的元素值必然是0，因为任何一个顶点与它自身是没有连接的。

 

对于一个无向图，如果 1 和 2有关联，则arr[1][2] 和 arr[2][1]都为1。对于一个有向图，如果 1 指向 2，但2不指向1，则arr[1][2]为1，arr[2][1]为0.

对于一个带权图，arr[i][j]的值就是权重，权重为0表示没有连接。

 

邻接矩阵的优点是快速查找两个节点的关系，时间复杂度O(1)；但占用大量空间，空间复杂度是O(n^2)。

 

领接表是一个数组arr，在逻辑上arr的每个下标存储着每个顶点对应的相邻顶点（对于拥有n个顶点的图，arr的长度就为n，arr[i]存储着 i 这个节点的所有相邻节点）。在物理上，arr[i]可以用一个链表或数组存储 i 这个节点的相邻节点。

 

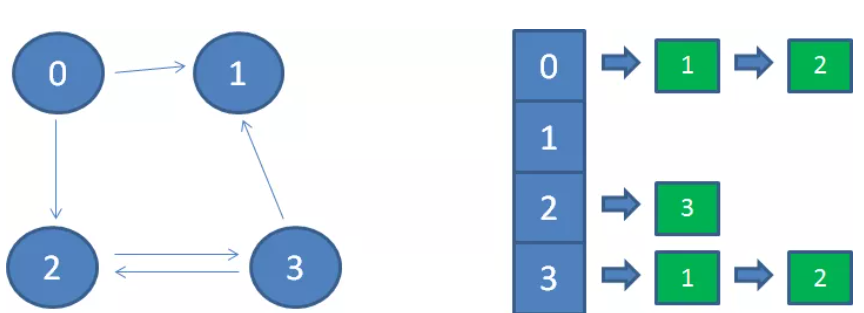
邻接表默认存储有向图，如果要存储一个无向图，则需要消耗多一倍的空间。例如 1 -> 2，对于有向图而言，arr[1]内需要包含2，但arr[2]不用包含1；但对于无向图而言，邻接表将其理解为双向，因此arr[1]内需要包含2，arr[2]内也需要包含1。

 

邻接表的优点是节省空间，空间复杂度O(n)，缺点是查找两个顶点是否相连较慢，时间复杂度为O(n)。而且对于有向图而言，邻接表可以以O(n)复杂度找到某个顶点所指向的相邻顶点，但要找到所有指向本顶点的其他顶点则需要遍历整个邻接表，复杂度为O(n^2)。

 

为了满足“找到所有指向本顶点的其他顶点”这个需求，描述一个图不仅需要维护邻接表，还需要维护逆邻接表。

 

逆邻接表 rarr 的结构和邻接表一模一样，只是rarr[i]存储的是指向 i 自己这个顶点的所有顶点。

 

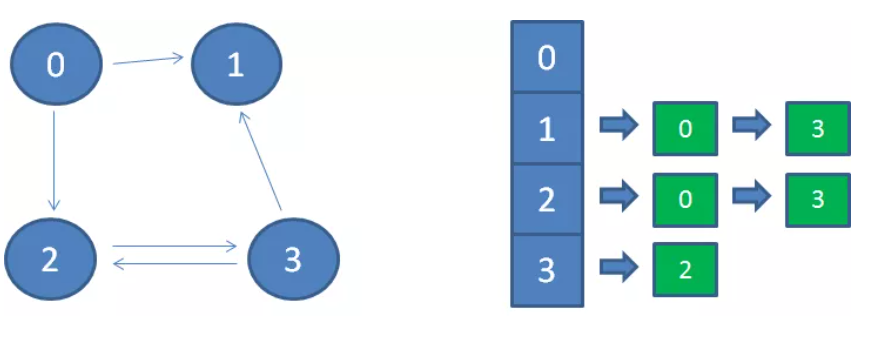
因此，一个图 = 邻接表 + 逆邻接表，如果没有“找到所有指向本顶点的其他顶点”这个需求，则只维护邻接表即可。

 

十字链表相当于邻接表和邻接链表的结合，其物理上也是使用一个数组arr表示，但 arr[i]应该保存一个对象，该对象保存两个数组（或者两个链表）分别用来表示 i 这个顶点指向的相邻顶点，和 i 被哪些顶点指向。

 

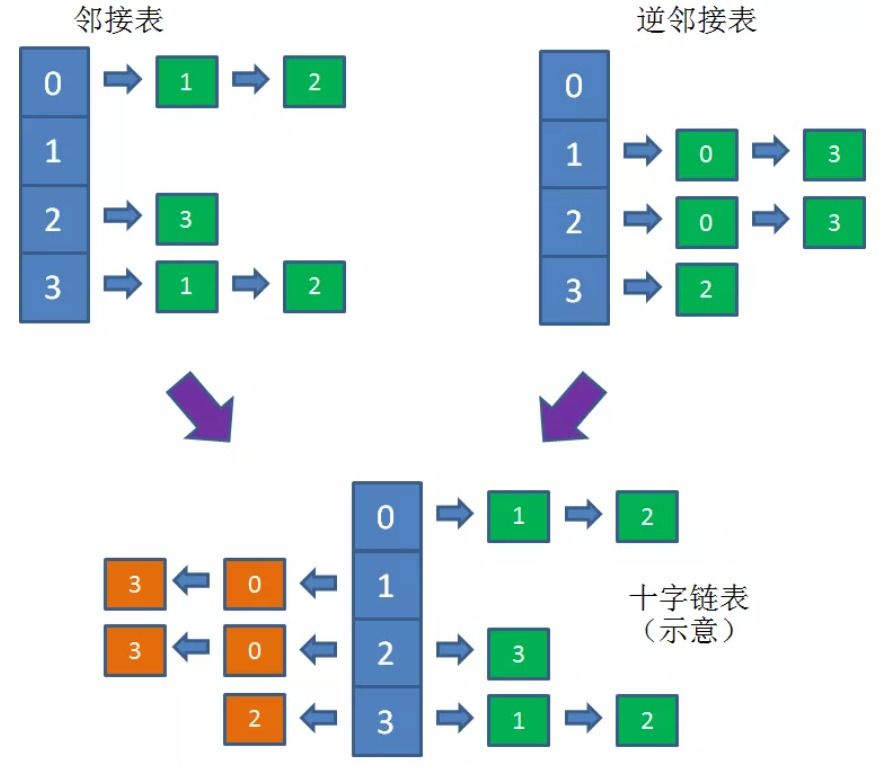
下面是以邻接表实现的图

// 有向图节点
type GNode struct{
	Val int
	Neibors []*GNode		// 某节点的相邻节点
}

func (gnode *GNode) init(val int) GNode{
	return GNode{Val: val, Neibors: make([]*GNode, 0)}
}

// 以邻接表方式表示的图
type Graph struct{
	Pos map[*GNode]struct{}	// 存储图的所有节点
}

// 将n1连向n2节点（有向）
func (graph *Graph) connect(n1, n2 *GNode) bool{
	if _, ok := graph.Pos[n1]; !ok{
		return false	// n1不在graph中则返回false
	}

	if _, ok := graph.Pos[n2]; !ok{
		graph.Pos[n2] = struct{}{}    // 将n2节点假如到 Graph 中
	}

	n1.Neibors = append(n1.Neibors, n2)
	return true
}

 

 

 

 

最小生成树算法

最小生成树算法的作用是将一个图的多余边去除，使得图中所有顶点满足连通性的同时，边的权重总和最小，此时这个取出多余边的图我们称为最小连通子图，最小连通子图没有回路，因此是一个树形结构，又称为最小生成树。

如果我们将每条边看成是一个顶点到达另一个顶点的成本，最小生成树算法的目的是将整个图所有节点连通的成本最小化。而最短路径算法则是算出任意两个节点连通的最小成本。

 

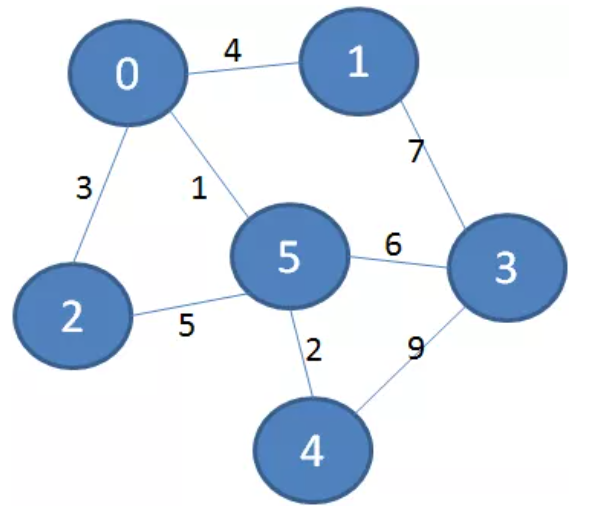
例如一个图原本的样子是这样

 

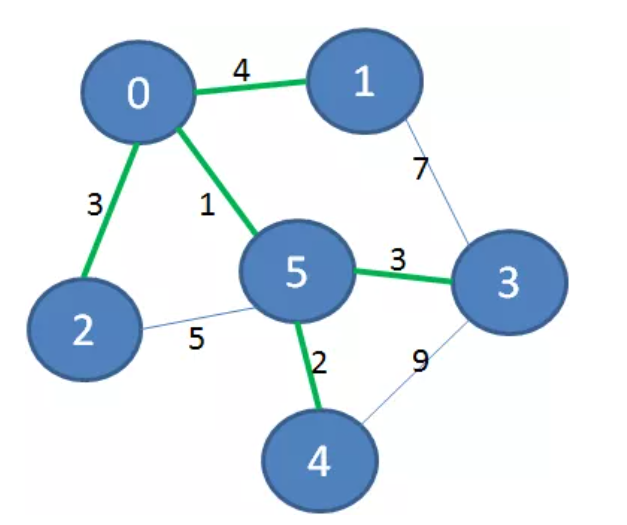
变成最小生成树后是这样

 

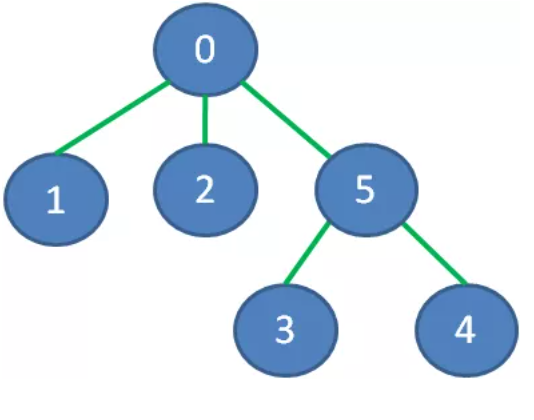
最小生成树算法采用贪心算法：

1、创建一个“已连通集合（已触达顶点集合）”用于存放已经遍历过并且加入到生成树的顶点。创建一个一维数组arr表示最小生成树，顶点 i 的父节点为 arr[i]。生成树arr有一个虚拟根节点 -1。

2、从图中任意选择一个顶点A加入到“已连通集合”，节点A作为 arr 的下标0，arr[0] = -1，即顶点A的父节点是虚拟节点 -1。

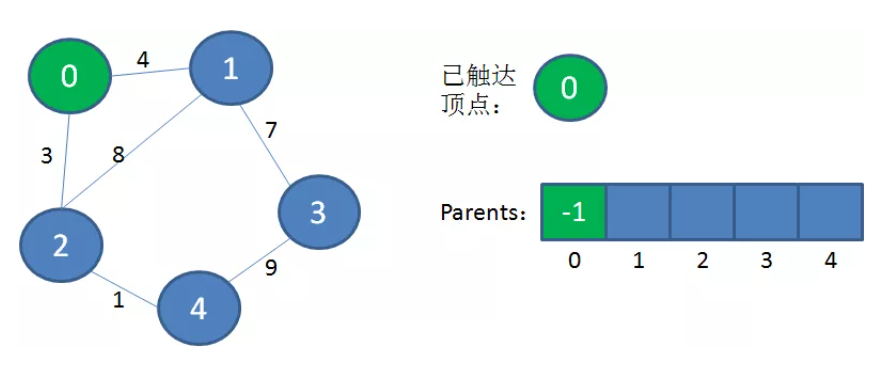
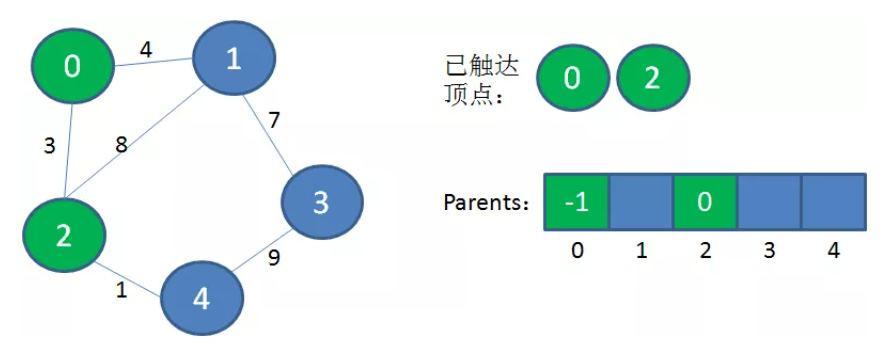
3、从“已连通集合”中选择一个from节点，要求from节点和from的未访问过的相邻节点to节点的距离最小。将to顶点加入到“已连通集合”和最小生成树中。

4、重复上述过程，直到原图的所有顶点都加入到“已连通集合”和最小生成树中。

 

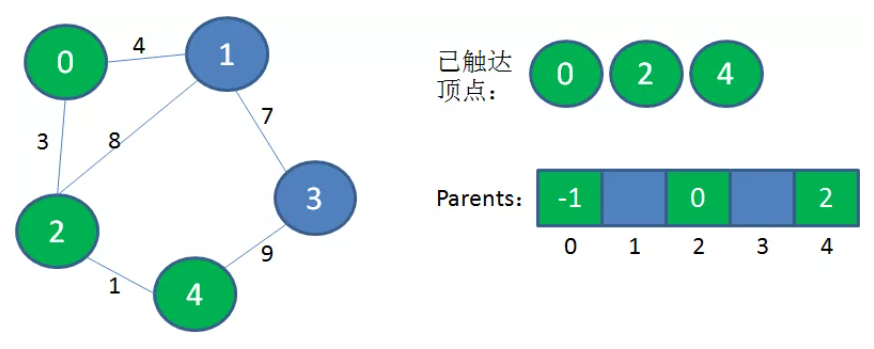
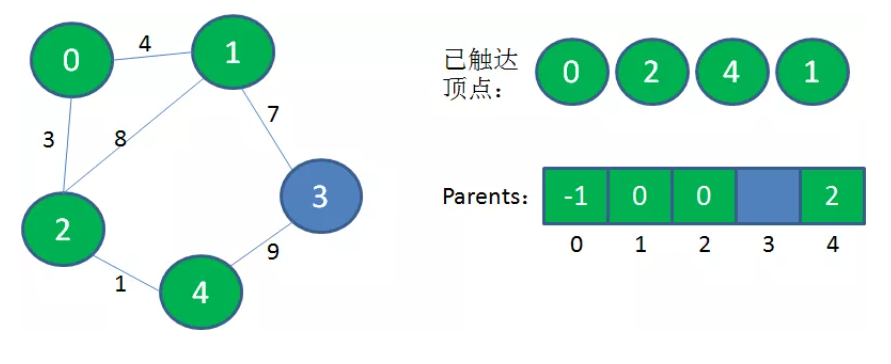
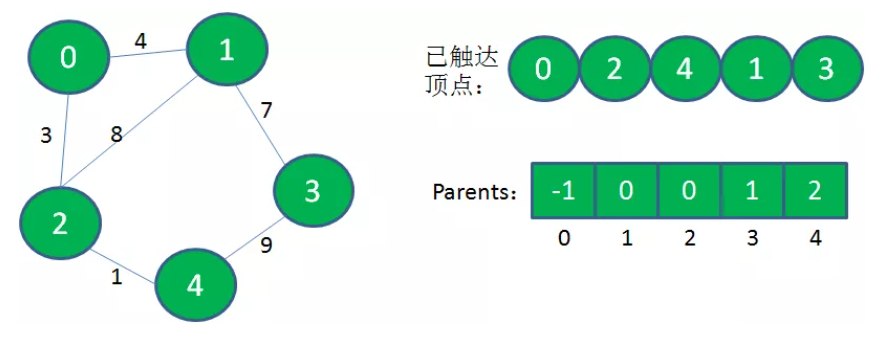
所生成的最小生成树的边的条数 = 总顶点数 - 1 = n - 1

 

代码实现如下：

// 最小生成树算法
func buildMinTree(g [][]int) []int{
	num := len(g)		// 顶点数
	minTree := make([]int, num)
	visited := make(map[int]struct{})	// 已连通集合

	curVext := 0	// 当前遍历到的，即将放入集合内的顶点
	minTree[curVext] = -1		// 将 0 号节点放入集合中
	visited[curVext] = struct{}{}

	for len(visited) < num{
		minWeight := math.MaxInt32		// 已连通集合的某节点 和 未连通的某节点 之间最小距离
		var from, to int
		for nextFromVext, _ := range(visited){	// 从已连通集合中选择一个from节点
			for nextToVext:=0; nextToVext<num; nextToVext++{	// 从所有from节点的相邻节点选择一个未访问的且距离最小的to节点作为下一个生成树节点
				if _, ok := visited[nextToVext]; !ok && g[nextFromVext][nextToVext] < minWeight{ // nextFromVext 到 nextToVext的距离小于 minWeight 既说明 这两个顶点是相邻的（因为他们的距离 比 MaxInt 小），又说明本nextToVext顶点比上一次的nextToVext顶点离 nextfromVext顶点近
					from = nextFromVext
					to = nextToVext
					minWeight = g[nextFromVext][nextToVext]
				}
			}
		}

		visited[to] = struct{}{}
		minTree[to] = from
	}
	return minTree
}


// 测试用例（用的是最短路径那个例子）
func TestBuildMinTree(t *testing.T) {
	m := math.MaxInt32
	matrix := [][]int{
		{0,5,2,m,m,m,m},
		{5,0,m,1,6,m,m},
		{2,m,0,6,m,8,m},
		{m,1,6,0,1,2,m},
		{m,6,m,1,0,m,7},
		{m,m,8,2,m,0,3},
		{m,m,m,m,7,3,0},
	}
	fmt.Println(buildMinTree(matrix))    // [-1 0 0 1 3 3 5]
}