我们知道计算机的内存有限，如果并发运行的进程所需的内存空间超过了物理内存的总和，就需要通过虚拟内存的技术将休眠的进程的内存空间或者将处于等待或运行进程的部分内存空间换出到磁盘。

操作系统需要使用特定的换入换出算法来管理内存实现上述过程。LRU算法（最近最少使用算法）就是一种比较常见的内存管理算法。

 

下面我们直接通过力扣的一道题目来了解LRU算法。

力扣146. LRU 缓存机制

运用你所掌握的数据结构，设计和实现一个  LRU (最近最少使用) 缓存机制 。

实现 LRUCache 类：

LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存

int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。

void put(int key, int value) 如果关键字已经存在，则变更其数据值；如果关键字不存在，则插入该组「关键字-值」。当缓存容量达到上限时，它应该在写入新数据之前删除最久未使用的数据值，从而为新的数据值留出空间。

你是否可以在 O(1) 时间复杂度内完成这两种操作？

 

题目给出类的框架如下

type LRUCache struct {
    
}
func Constructor(capacity int) LRUCache {
}
func (this *LRUCache) Get(key int) int {
}
func (this *LRUCache) Put(key int, value int)  {
}
/**
 * Your LRUCache object will be instantiated and called as such:
 * obj := Constructor(capacity);
 * param_1 := obj.Get(key);
 * obj.Put(key,value);
 */

 

分析：

1、题目希望get和put以O(1)复杂度访问key，因此需要使用到hashmap。

2、LRU在缓存已满的情况下淘汰最久未使用的key，这里可以使用一个容量为capacity的双向链表的队列描述最近访问的capacity数量个key的顺序，队列中的节点按照访问时间的先后排列，队首是最久未使用的key，队尾则是最近使用过的key。节点包含key和value两个属性。

一开始缓存没满的时候，执行get(key)或者put(key, val)会将key从队列中间取出并放回链表尾部。当缓存满了的时候，将队首的key弹出，将新key链入队尾。

3、单纯的链表无法直接找到中间的某个节点，只能顺序查找，复杂度为O(n)。为了实现O(1)复杂度找到key对应的节点在链表的位置，可以在hashmap中以key为索引，以key对应的节点的指针为值。而链表节点则存储数据的key和val以及向前和向后指针。

这种 hashmap和双向链表组合而成的数据结构被称为“哈希链表”，也是LRU算法的核心数据结构。

 

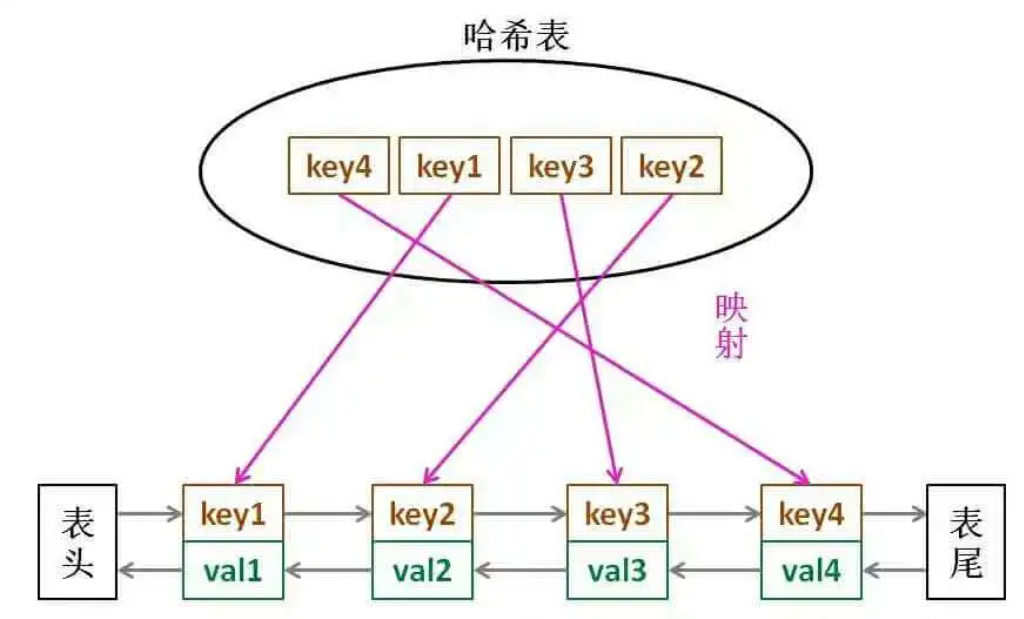
Get()要做的事情就是通过key从hashmap找到目标节点，将目标节点放到队列尾部（即更新其使用时间为最新），最后返回该节点的值即可。

 

Put()要做的事稍微复杂，建议画好流程图再写代码可以一目了然。

 

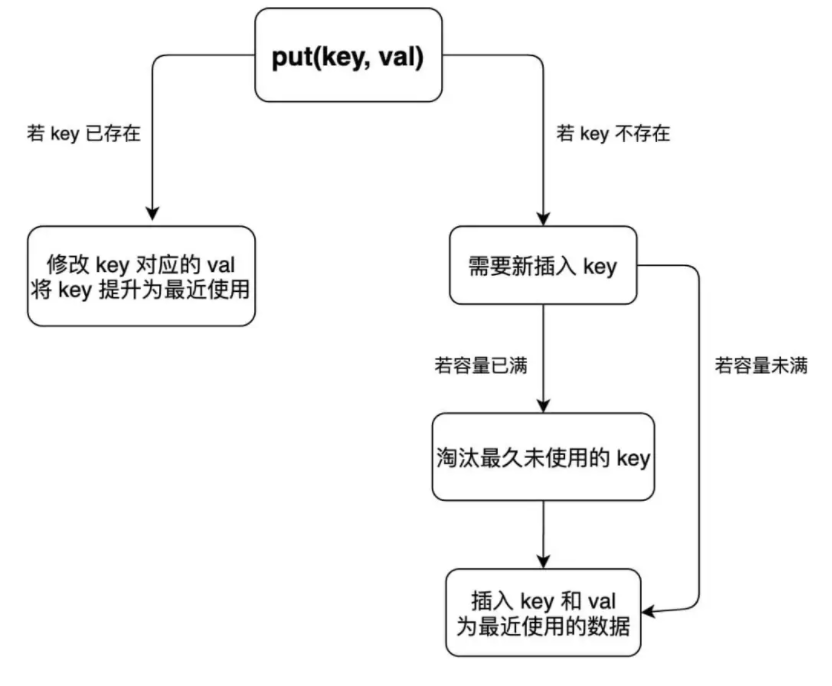
代码实现如下：

type LRUCache struct {
   capacity int
   nodeMap map[int]*IntNode
   linkedlist *DoubleLinkedList
}


func LRUConstructor(capacity int) LRUCache {
   nodeMap := make(map[int]*IntNode)
   linkedlist := initDoubleLinkedList()
   cache := LRUCache{
      capacity: capacity,
      nodeMap: nodeMap,
      linkedlist: linkedlist,
   }
   return cache
}


func (this *LRUCache) Get(key int) int {
   node, ok := this.nodeMap[key]
   if !ok{
      return -1
   }
   this.moveNode2Tail(node)
   return node.Val
}


func (this *LRUCache) Put(key int, value int)  {
   if node, ok := this.nodeMap[key]; ok{     // 缓存中存在该节点，更新节点的值
      node.Val = value
      this.moveNode2Tail(node)
   }else{ // 新增
      if this.linkedlist.Length >= this.capacity{    // 容量已满
         this.removeLeastRecent()      // 弹出链表的首部节点
      }
      this.addNewNode(key, value)    // 添加新节点
   }
}

// 将某个节点移到尾部
func (this *LRUCache) moveNode2Tail(node *IntNode){
   if node == this.linkedlist.Tail{   // 如果node本身就是最后一个节点则不操作
      return
   }

   if node.Prev != nil{
      node.Prev.Next = node.Next
   }else{ // 说明node是头部节点，应该把Head指针指向下一个节点
      this.linkedlist.Head = node.Next
   }

   node.Next.Prev = node.Prev
   node.Next = nil
   node.Prev = this.linkedlist.Tail
   this.linkedlist.Tail.Next = node
   this.linkedlist.Tail = node
}

// 移除最久未使用的节点
func (this *LRUCache) removeLeastRecent(){
   leastNode := this.linkedlist.shift()      // 先删除链表的首部节点
   delete(this.nodeMap, leastNode.Key)          // 再删掉hashMap中的key
}

// 添加新节点
func (this *LRUCache) addNewNode(key int, value int){
   newNode := this.linkedlist.append(key, value)
   this.nodeMap[key] = newNode
}

 

这段代码中双向链表的插入和删除方法有些麻烦，需要判断很多边界情况诸如移除的节点是首部或者尾部节点，或者当链表节点只有一个或零个的的情况下添加或删除节点。

为了避免这些麻烦，可以定义两个虚拟头尾节点，其key和value都是0，Head指针指向虚拟头部节点，Tail指向虚拟为节点，如果要获取链表的真实头部节点只需返回 linkedList.Head.Next 即可。通过定义两个虚拟头尾节点可以减少很多临界情况的判断。

 

如下所示：

/** 双向链表 **/
type DoubleLinkedList struct{
   Head *IntNode     // 头部节点
   Tail *IntNode     // 尾部节点
   Length int    // 节点数
}

func initDoubleLinkedList() *DoubleLinkedList{
   linkedList := DoubleLinkedList{}
   linkedList.Head = &IntNode{}   // 虚拟头尾节点
   linkedList.Tail = &IntNode{}
   linkedList.Head.Next = linkedList.Tail
   linkedList.Tail.Prev = linkedList.Head
   return &linkedList
}

// 移除某个节点
func (ll *DoubleLinkedList) remove(node *IntNode) *IntNode{
   if node.Prev != nil{
      node.Prev.Next = node.Next
   }

   if node.Next != nil {
      node.Next.Prev = node.Prev
   }

   ll.Length--
   return node
}

// 从头部弹出一个节点
func (ll *DoubleLinkedList) shift() (deleteNode *IntNode){
   if(ll == nil || ll.Length == 0){
      return
   }

   return ll.remove(ll.Head.Next)
}

// 往后插入一个节点
func (ll *DoubleLinkedList) append(key, val int) *IntNode{
   if(ll == nil){
      ll = initDoubleLinkedList()
   }

   node := InitIntNode(key, val)
   ll.appendNode(node)
   return node
}

func (ll *DoubleLinkedList) appendNode(node *IntNode) *IntNode{
   if(ll == nil){
      ll = initDoubleLinkedList()
   }

   lastNode := ll.Tail.Prev
   lastNode.Next = node
   ll.Tail.Prev = node
   node.Prev = lastNode
   node.Next = ll.Tail
   ll.Length++
   return node
}

func (ll *DoubleLinkedList) getHead() *IntNode{
   if ll.Length == 0{
      return nil
   }
   return ll.Head.Next
}

func (ll *DoubleLinkedList) getTail() *IntNode{
   if ll.Length == 0{
      return nil
   }
   return ll.Tail.Prev
}