前缀树是一棵存储字符串的多叉树。

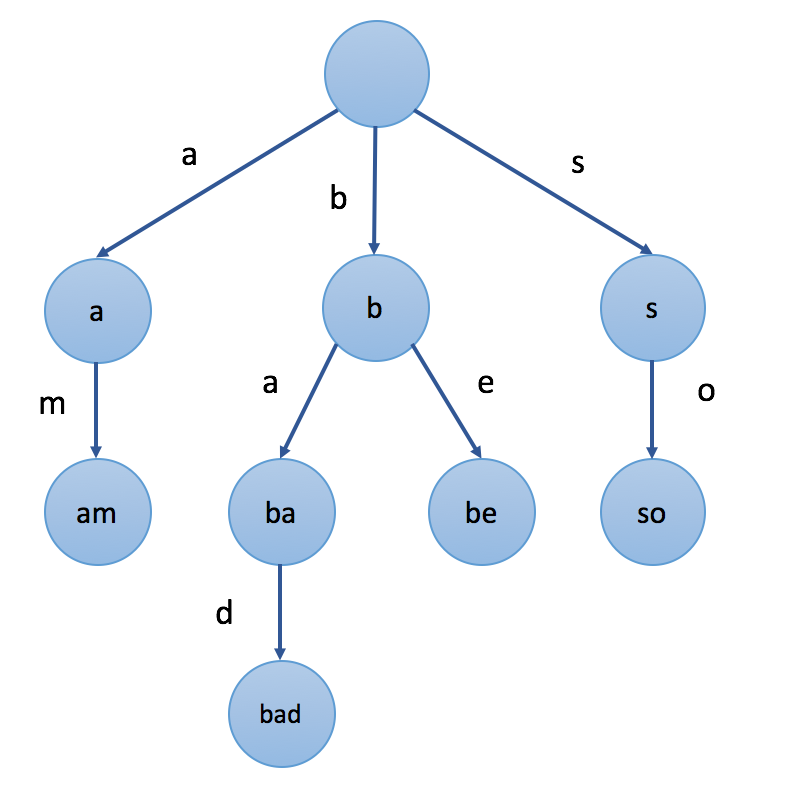
· 前缀树特征

前缀树的节点存储字符串（不是真的存储一个字符串，而是代表一个字符串），节点之间的路径存储字符。

一个节点A代表的字符串 由从根节点到节点A之间的路径所存的字符拼接组成。

一个节点A代表的字符串和A的所有后代节点所代表的字符串具有相同前缀，因此称为前缀树。

根节点代表的字符串是空字符串。

 

如果要往前缀树存储一个单词 "apple"，则会该前缀树会创建5个节点分别代表 "a"，"ap"，"app", "appl" 和 "apple" 这5个字符串。

 

· 前缀树的表示

前缀树的一个节点是一个对象，节点对象中可以使用数组或者hashmap存储它的多个子节点。

 

如果使用数组，可以申请一个大小为26的数组，代表字母a-z，数组存储的是子节点的地址。

type Trie struct {
    children [26]*Trie
    isEnd    bool
}

 

如果使用hashmap，则key存储本节点A到某一个子节点B路径上的字符，value存储子节点B的地址。

type Trie struct {
	children map[byte]*Trie		// 本节点的子节点
	isEnd bool	// 是否是个单词
}

 

需要注意

isEnd 表示本节点代表的字符串是否是一个串的结束（是否是一个完整单词），true表示是一个完整的单词，false表示它只是一个前缀。

前缀树节点不需要用一个成员属性来存储父节点到本节点路径上的字符，这个字符已经存到父节点的children属性中。

使用数组存储比使用hashmap存储，其访问速度更快，浪费更多空间。

 

前缀树实现：

type Trie struct {
	sons map[byte]*Trie		// 本节点的子节点
	word bool	// 是否是个单词
}


func TrieConstructor() Trie {
	sons := make(map[byte]*Trie)
	return Trie{sons: sons}
}


func (this *Trie) Insert(word string)  {
	curNode := this
	for _, char := range([]byte(word)){
		if _, ok := curNode.sons[char]; !ok{
			newNode := TrieConstructor()
			curNode.sons[char] = &newNode
		}
		curNode = curNode.sons[char]   //进入到以char结尾的前缀树节点
	}
	
	// 前缀树中存储本单词的节点word属性为true表示该节点是个完整的单词
	curNode.word = true
}


func (this *Trie) Search(word string) bool {
	targetNode := this.findString(word)
	if targetNode == nil{	// 说明没有找到word这个字符串在前缀树中对应的节点
		return false
	}

	// 节点targetNode存储的是传入的参数word这个字符串，但A可能存的是前缀不是单词，也可能是单词不是前缀
	return targetNode.word
}


func (this *Trie) StartsWith(prefix string) bool {
	targetNode := this.findString(prefix)
	if targetNode == nil{
		return false
	}
	return true
}

// 查找目标字符串所在的节点，可以是个前缀或完整单词
func (this *Trie) findString(str string) *Trie{
	curNode := this
	for _, char := range([]byte(str)){
		if _, ok := curNode.sons[char]; !ok{
			return nil
		}
		curNode = curNode.sons[char]
	}

	// 走出遍历的时候，curNode刚好位于叶子节点，走不出遍历说明 前缀树不存在存储str这个字符串的节点
	return curNode
}

 

· 前缀树的时间和空间复杂度

前缀树的查找和插入的时间复杂度只与要插入和查找的字符串长度有关，和前缀树有多少个节点无关，目标字符串长度为N则时间复杂度为O(N)。

使用数组表示子节点时，假设数组长度为m（m一般为26），树的平均高度为n，考虑最坏的情况就是每个节点的每个数组元素都不为空，则前缀树的空间复杂度为O(m^n)，即26的n次方。

 

· 关于前缀树的应用

如判断一个单词是否正确，单词自动补全，单词替换等。

解法1：直接使用类似strWith()的方法，但是题目要求要用最短词根替换，因此需要将dictionary按照元素长度升序排序。

import (
	"sort"
	"strings"
)

func replaceWords(dictionary []string, sentence string) string {
	sortDictionary := dictionarySort(dictionary)
	sort.Sort(sortDictionary)
	arr := strings.Split(sentence, " ")
	for i, word := range(arr){
		for _, prefix := range(sortDictionary){
			if strings.HasPrefix(word, prefix){
				arr[i] = prefix
				break
			}
		}
	}
	return strings.Join(arr, " ")
}

type dictionarySort []string
func (this dictionarySort) Len() int{return len(this)}
func (this dictionarySort) Less(i, j int) bool{return len(this[i]) < len(this[j])}
func (this dictionarySort) Swap(i, j int) {this[i], this[j] = this[j], this[i]}

该方法的时间复杂度为 O(NM)，N是sentence的长度，M是词根个数。空间复杂度为O(N+M)。

 

解法2：前缀哈希，将所有词根放入到一个set集合中，按sentence的每个单词的所有词根从set寻找是否存在该词根，如果存在则替换

func replaceWords2(dictionary []string, sentence string) string {
	hashmap := make(map[string]struct{})
	for _, dic := range(dictionary){
		hashmap[dic] = struct{}{}
	}

	res := ""
	for _, word := range(strings.Split(sentence, " ")){
		replace := false
		for i:=1; i<=len(word); i++{
			prefix := word[:i]
			if _, ok := hashmap[prefix]; ok{
				res += prefix + " "
				replace = true
				break
			}
		}
		if !replace {
			res += word + " "
		}
	}
	return strings.TrimRight(res, " ")
}

时间复杂度为 O(∑w[i]^2)，w[i]表示sentence的第i个单词，因此复杂度为所有单词长度的平方和。空间复杂度O(M)，M是词根总长度。

 

解法3：前缀树，根据dictionary构建前缀树，使用双指针 i, j 遍历sentence中的单词，在前缀树中查找sentence[i:j]这个前缀是否存在。

func replaceWords(dictionary []string, sentence string) string {
	trie := TrieConstructor()
	for _, dic := range(dictionary){
		trie.Insert(dic)
	}

	res := ""
	i, j:= 0, 0
	_posToNextWord := func(){
		for j < len(sentence) && sentence[j] != ' '{
			j++
		}
	}


	for j < len(sentence){
		_posToNextWord()
		res += trie.ContainWord(sentence[i:j]) + " "
		j++
		i=j
	}
	return strings.TrimRight(res, " ")
}

type Trie struct {
	Children map[byte]*Trie		// 本节点的子节点
	IsEnd bool	// 是否是个单词
}


func TrieConstructor() Trie {
	Children := make(map[byte]*Trie)
	return Trie{Children: Children}
}


func (this *Trie) Insert(word string)  {
	curNode := this
	for _, char := range([]byte(word)){
		if _, ok := curNode.Children[char]; !ok{
			newNode := TrieConstructor()
			curNode.Children[char] = &newNode
		}
		curNode = curNode.Children[char]
	}

	// 前缀树中存储本单词的节点word属性为true表示该节点是个完整的单词
	curNode.IsEnd = true
}

// 返回str在前缀树中的最小词根
func (this *Trie) ContainWord(str string) string{
	substr := make([]byte, 0)
	curNode := this
	for _, char := range([]byte(str)){
		if curNode.Children[char] == nil{
			return str
		}
		substr = append(substr, char)
		curNode = curNode.Children[char]
		if curNode.IsEnd{
			return string(substr)
		}
	}
	return str
}

该算法的时间和空间复杂度都是O(N)，N是sentence的长度。